Inscription / Connexion Nouveau Sujet
fonctions
Bonjour, j'ai besoin d'aide. Merci beaucoup
Voilà ce que j'ai trouvé. Est ce exact?
1)
f'(4) =2
f'(-1)=0
f(4) = -3
2) y=2(x-4)+(-3)
y= 2x-8-3
y=2x-11
3) f(x)=0 admet 3 solutions (-3,1 et 5)
f'(x) = 0 admet 3 solutions (3,-3 et 1)
f'(x) <-0 admet 2 solutions (-1 et 2)
4)x -4 -3 -1 1 3 5 6
4 5
0
f(x) -5 0 0
-4
je n'arrive pas à faire le tableau de signe de f'
Partie B
La partie B je comprends pas
Merci pour vos réponses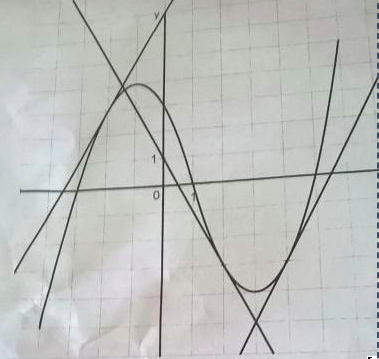
**malou edit > image recadrée sur la figure, merci de faire l'effort de recopier ton énoncé si tu veux de l'aide**conformément à ![]() Sujet ancien- ne plus donner ce lien-merci**
Sujet ancien- ne plus donner ce lien-merci**
C'est pas mal mais j'ai relevé des erreurs :
f'(x) = 0 admet 3 solutions (3,-3 et 1)
heu non -1 et 3
f'(x) <-0 admet 2 solutions (-1 et 2)
pas du tout. c'est une inégalité, les solutions sont des intervalles (ceux dans lesquels la dérivée est négative dont ceux dans lesquels la fonction est décroissante)
Bonjour,
Pour le tableau de signes, il y a un excellent outil en cliquant sur le Ltx juste à gauche de  sur la barre d'icônes sous la zone où l'on écrit
sur la barre d'icônes sous la zone où l'on écrit
Une fenêtre s'ouvre , cliquer alors sur "tableau de variations"
Bonjour Wham, j'ai essayé mais je n'arrive pas à insérer le tableau. Néanmoins, est ce que mes réponses sont exactes?
Voici l'énoncé,
Partie A : On suppose que la courbe représente une fonction f. Les droites sont tangentes à la courbe.
1) par lecture graphique, déterminer f'(4), f'(-1), f(4)
2) Déterminer l'équation de la tangente à la courbe au point d'abscisse 4
3) Résoudre les équations f(x) = 0, f'(x) = 0, f'(x) <-0
4) Construire le tableau de variations de f et le tableau de signe de f'
Partie B : On suppose maintenant que la courbe représente une fonction dérivée f'
Construire le tableau de variation de f et le tableau de signe de f'
MERCI GLAPION
Merci pour vos nouvelles réponses afin de compléter ce qui me manque
Bonjour, j'ai besoin d'aide pour f'(x)<-0. Est ce que l'intervalle est [2;3]?
Et pour la 4) Tableau de signe de f'
Et Partie B
Merci beaucoup 😊
f'(x) 0 c'est donc l'intervalle où la fonction est décroissante
0 c'est donc l'intervalle où la fonction est décroissante
donc [-1;3] plutôt
et après ça le tableau de signe d f'(x) est facile à faire, négatif dans [-1;3] et positif partout ailleurs.
Partie B. Maintenant c'est la courbe (anciennement f) que l'on considère comme la dérivée d'une autre fonction. Donc regarde quand est-ce qu'elle est positive et négative et déduis en les variations de cette autre fonction.
Bonjour,
4) tableau de signe de f'
x -l'infini -3 1 5 + l'infini
| | |
f'(x) - 0 + 0 - 0 +
Est ce exact ? merci de votre aide
Partie B
Tableau de variation
x -l'infini -1 4 + l'infini
2 + l'infini
0 /
f(x) -l'infini
Tableau de signe
x -l'infini -1 4 + l'infini
f'(x) - 0 +
Est ce bon?
non le tableau de signe de f', je t'avais dit : "négatif dans [-1;3] et positif partout ailleurs.", c'est pas ce que tu as fait ??
partie B, je ne comprends pas ce que tu as fait 
tu vois le signe de f'(x) sur le dessin, non ? quand est-ce que la courbe est au dessus de l'axe et quand est-ce qu'elle est en dessous ?
oui, moi aussi je n'ai rien compris Je vais attendre la correction du prof pour essayer de comprendre. Merci encore pour ton aide
Je vais attendre la correction du prof pour essayer de comprendre. Merci encore pour ton aide
C'est simple, tu vois sur le dessin quand est-ce que la dérivée est positive ou négative et tu en déduis quand est-ce que la fonction est croissante ou décroissante.



