Inscription / Connexion Nouveau Sujet
fonctions, tableau de variations/signe, tangente
Bonjour,
j'ai un exercice que je n'arrive pas à résoudre car je n'en ai jamais fait de ce type en classe, pouvez-vous m'aider?
Voici l'énoncé:
f est une fonction définie pour tout x différent de 1 par:f(x)= (ax²+bx+c)/(x-1)
On appelle Cf la courbe représentant f dans un repère orthonormé.
1) Déterminer les réels a, b et c sachant que:
- la courbe Cf passe par les points de coordonnés (-1; -6) et (2; 0)
- la tangente à la courbe Cf au point d'abscisse 0 est parallèle à la droite d'équation y= -x
2) Combien la courbe Cf possède t-elle de tangentes parallèles à cette droite d'équation y= -x ? Donner leurs équations.
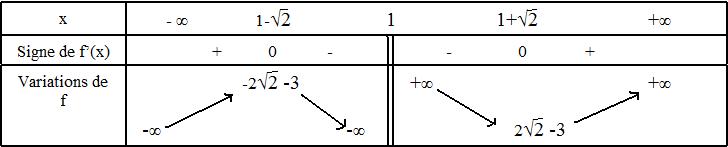
3) Justifier tous les renseignements fournis dans le tableau de variation de f. (Voir tableau)
4) a) Démontrer que la courbe admet deux droites asymptotes, dont une, oblique, que l'on appellera D.
b) Etudier, suivant les valeurs de x, la position relative de Cf et D.
5) Démontrer que la courbe Cf amdet un centre de symétrie.
Si vous pouvez m'aider, déjà pour la question 1, car du coup, elle me bloque pour les autres.
Cordialement
Bonjour,
Pour la 1), il faut trouver un système d'équations et le résoudre.
Ici :
- la courbe Cf passe par les points de coordonnés (-1; -6) et (2; 0)
=> f(-1) = -6 et f(2) = 0
- la tangente à la courbe Cf au point d'abscisse 0 est parallèle à la droite d'équation y= -x
=> Cela veut dire qu'ils ont le même coefficient directeur. Or, la dérivée en un point donne le coefficient directeur en ce point. Donc f'(0) = -1.
Merci de votre réponse mais je ne vois pas ou vous voulez en venir?
Pouvez vous être plus précis(e)?
SVP
Bonjour,
grace à vos renseignements j'ai trouvé:
f(-1)= a+b+c/-2
f(2)= 4a+2b+c
f(0)= -c
Que dois-je faire après?
Bonjour,
Tu as trouvé que :
f(-1)= a+b+c/-2
f(2)= 4a+2b+c
f(0)= -c
Mais il semble y avoir des erreurs car, pour tout x réel différent de 1, f(x)= (ax²+bx+c)/(x-1) ; donc :
f(-1) = (a(-1)² + b(-1) + c)/(-1 - 1) = (a - b + c)/(-2)
f(2) = (a2² + b2 + c)/(2 - 1) = (4a + 2b +c)/1 = 4a + 2b + c
Comme f '(x) = [(2ax + b)(x - 1) - 1(ax² + bx +c)]/(x - 1)² = (2ax² - 2ax + bx - b)/(x - 1)², alors :
f '(0) = (-b)/(-1)² = -b
Or :
f(-1) = -6
f(2) = 0
f '(0) = -1
Donc :
(a - b + c)/(-2) = -6
4a + 2b + c = 0
-b = -1
A toi de résoudre ce système de 3 équations à 3 inconnues  .
.


