Bonjour pappus

et bienvenue...

en 2023 tu t'es inscrit, et je vois comme profil "doctorat"
là je vois que tu postes niveau terminale (cette question pour moi n'est pas du niveau terminale)
Peut-on en savoir un peu plus sur ton véritable profil et sur la finalité de cette question que tu poses aujourd'hui afin que ceux qui vont te répondre collent au mieux à tes connaissances
merci

Bonjour pappus et bienvenue sur l'

Bonjour malou

Bonjour Kohle

Oui, après avoir posté mon message, me suis dit, Pappus...une question de géométrie et Kohle qui pointe le bout de son nez...

Compris

Je bouge le sujet et le met en détente

Merci malou
Petit problème auquel on ne peut pas grand chose : tel que je connais l'ami pappus, il va croire que son message a disparu ...

Bonjour pappus,
Je me suis peut-être trompé précédemment en interprétant ton énoncé (avec le pluriel "... les normales ...")
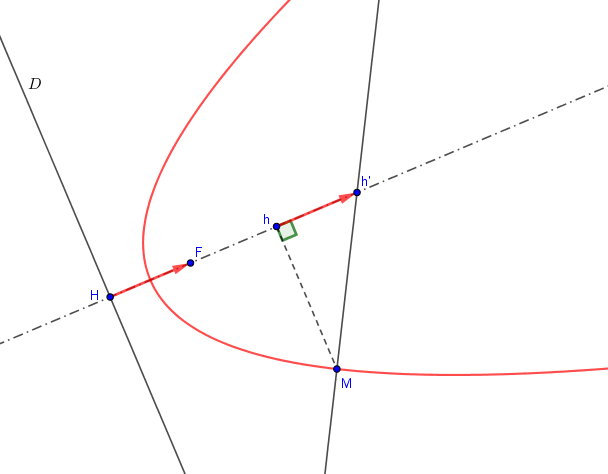
Une figure lorsque le point appartient à la parabole sans passer par la tangente :

 Cliquez pour afficher

Les sous normales sont égales au paramètre :

Amitiés.

Ben comme il a activé les notifications il va directement arriver sur la discussion par le lien qu'il va avoir dans sa messagerie...

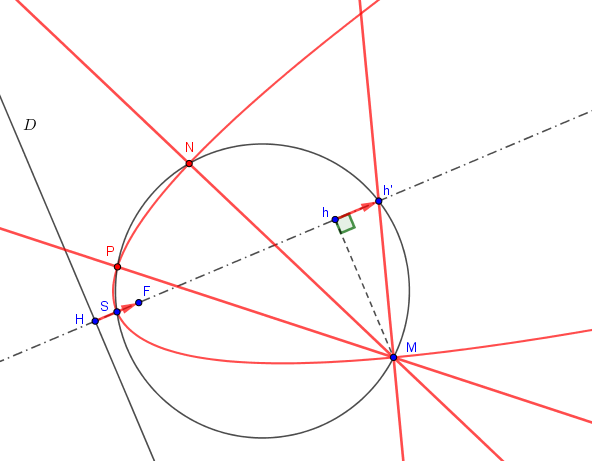
Je viens  de me souvenir que des normales issues de , il y en a deux autres.
Y'a queq chose qui cloche la dedans : j'y retourne immédiatement

Finalement une figure dans le cas où existent 3 normales passant par :

 Cliquez pour afficher

- la première est obtenue avec la sous normale égale au paramètre en
-Les deux autres avec les points et intersections du cercle et de la parabole où est son sommet.

Bonsoir,
L'énoncé demandait une construction géométrique (règle et compas). L'intersection d'une parabole et d'un cercle aboutit généralement à une équation de degré 4 donc inconstructible.
Ici, on connaît deux points d'intersection : et donc du second degré constructible.
Une nouvelle figure où on peut oublier le cercle :

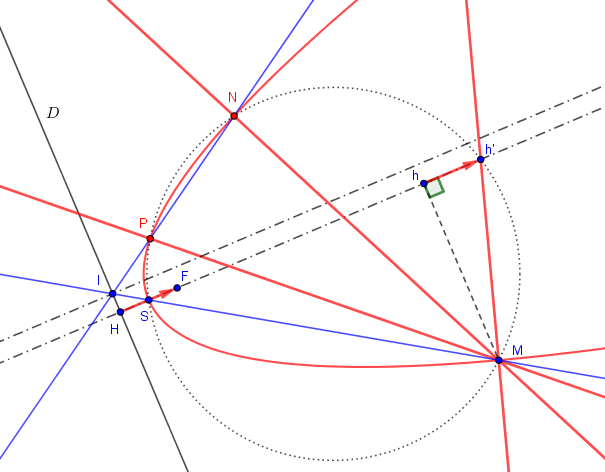
La droite coupe la directrice en
La droite est symétrique de par rapport à la parallèle à l'axe passant par
Reste à construire les intersections de cette droite  avec la parabole. Un problème connu pour lequel on peut consulter le Lebossé &Hémery de mathélem.

Bonjour à tous
Je suis tout nouveau sur ce forum et j'avais l'habitude de poser des questions de géométrie d'un niveau bien supérieur à celui de Terminales sur les-mathematiques.net, étant agrégé de Mathématiques.
Comme cette géométrie n'est plus enseignée depuis longtemps, j'ai voulu donner pour commencer une question plus simple sans être tout à fait sûr qu'elle soit dans le programme de Terminales.
La parabole est un graphe, donc en principe ses tangentes et donc ses normales sont dans le programme de Terminales.
Formuler analytiquement le problème par contre est une question peu courante pour un élève lambda.
On tombe sur une équation du troisième degré en général dont on connait une solution évidente dans le cas particulier envisagé.
Il reste une équation du second degré, donc en principe les pieds des normales cherchées sont constructibles à la règle et au compas.
Il faut quand même donner une construction quelle qu'elle soit.
Amicalement
pappus

Bonsoir à tous
Construire à la règle et au compas les normales à une parabole issues d'un point M de cette parabole

La solution de Kohle est exacte et très jolie.
Il reste quand même à la justifier géométriquement et ce n'est pas à la portée d'un élève de Terminales actuel qui ne connait que la géométrie analytique la plus élémentaire.
La construction issue naturellement des calculs n'est pas celle du Lebossé-Hémery mais est évidemment du même acabit.
Amicalement
pappus
PS
Que dois-je faire pour poster mes figures?

Bonsoir

Pour poster une image on clique sur Img sous la zone d'écriture et on télécharge son image
On peut cliquer sur aperçu avant de poster pour vérification
😉

Bonjour à tous
Construire à la règle et au compas les normales à une parabole issues d'un point M de cette parabole.

J'essaye d'insérer pour la première fois une figure pour le moment sans commentaires.
J'espère qu'elle a la taille autorisée sans en être sûr!
Amicalement
pappus

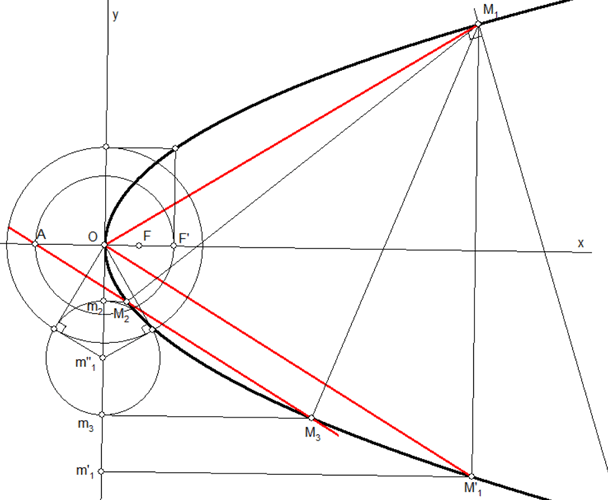
Bonjour pappus et merci pour cette belle figure.
Je pense l'avoir comprise. :
Une parabole d'équation où on part du point et de son symétrique par rapport à l'axe .
Le point a pour abscisse et on trace la parallèle à ) passant par qui coupe la parabole aux points et cherchés.
Tu as poussé le souci du détail en indiquant la construction permettant d'obtenir les intersections de cette droite avec la parabole.
Ma construction ressemble à la tienne (pour moi le point sur la directrice, pour toi le point sur l'axe).
J'avais plus ou moins justifié la mienne en me bornant à une vérification pas très satisfaisante sur la parabole d'équation : les normales en et passaient bien par le point (après conjecture GeoGebra).
Amitiés.

J'ai oublié de signaler que ton point est bien meilleur que mon point dans la mesure où il est fixe !

Bonjour à tous
Bien sûr ma figure que je commenterai à la fin de mes calculs est celle que pourrait produire un bon élève de Terminales d'aujourd'hui sans avoir connaissance du livre de Lebossé-Hémery qui appartient à l'histoire désormais.
Je vais travailler avec l'équation réduite de la parabole;

Son foyer est le point et sa directrice la droite d'équation:
Je ne sais pas si ces notions de foyer et de directrice sont au programme de Terminales. Je fais comme si!
Dans la suite j'aurais besoin de l'équation de la droite joignant les points et   de la parabole, d'ordonnées respectives   et
Il est facile de voir que cette équation est:

Je m'arrête provisoirement ici car il faut que je m'habitue à ces balises nouvelles pour moi qui entourent le texte en
Je note que le texte en   apparait avec un petit décalage horizontal vers le haut un peu désagréable.
Amicalement
pappus

Bonjour,

On peut toujours, par rotation et translations, ramener la parabole à l'équation y = a.x²  

On montre alors qu'il peut y avoir jusqu'à 3 points sur la parabole tels que des normales à la parabole passent par un point M(X,a.X²) choisi sur cette parabole.

Les abscisses de ces 3 points sont :

a)  x1 = X
b)  x2 = -X/2 - sqrt(X²/4 - 1/(2a²))
c)  x3 = -X/2 + sqrt(X²/4 - 1/(2a²))

Il n'y aura qu'une seule normale possible (le (a)) si X²/4 - 1/(2a²) < 0
Il y aura deux normales possibles si X²/4 - 1/(2a²) = 0
Il y aura trois normales possibles si X²/4 - 1/(2a²) > 0

exemple numérique :

a = 1
X = 2,2

On calcule x1 = 2,2 ; x2 = -1,943 et x3 = -0,257

J'ai placé ces points en rouge sur le dessin ...

Et j'ai fait la construction pour vérifier si les points rouges étaient bien placés.

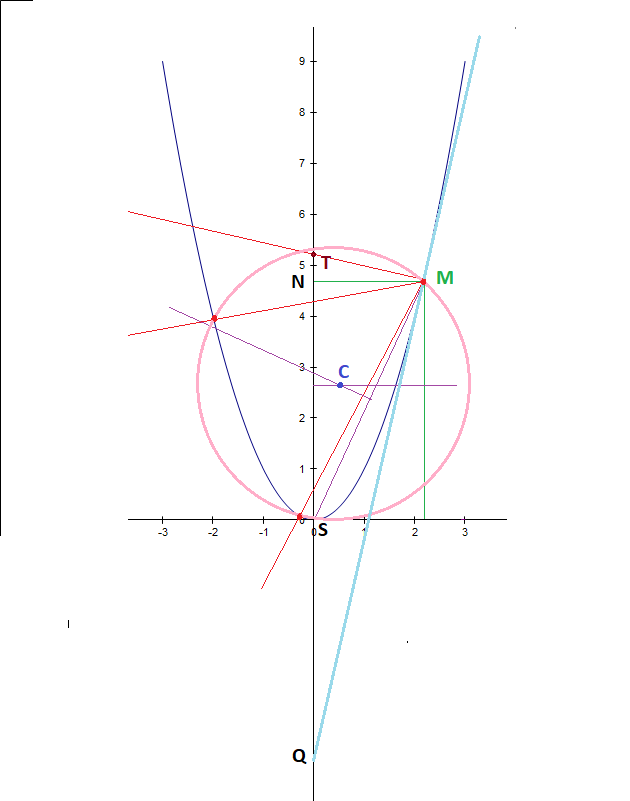
Construction :

On place N (ordonnée de M)
On olace Q tel que SQ = NS
On trace QM qui est la tangente à la parabole en M
On trace la perpendiculaire en M à la droite (QM) ... c'est la normale (celle qui existe toujours)

Soit T le point de rencontre de la normale ci dessus avec l'axe principal de la parabole.
On trace la médiatrice de TS
On trace la médiatrice de SM

Soit C le point de rencontre de ces 2 médiatrices
On trace le cercle de centre C et de rayon CM
Ce cercle passe par les points M2 et M3 de la parabole.

Les droites (MM2) et (MM3) sont aussi des normales à la parabole passant par M

Avec d'autres exemples numériques ... on aurait pu n'avoir que 1 ou 2 normales

Bonne nuit à tous

Construire à la règle et au compas les normales à une parabole issues d'un point M de cette parabole.

La figure de candide2 est intéressante et rejoint celle de Kohle en traçant le cercle circonscrit au triangle .
Mais il n'y a pas  de justification proprement dite.
Le point crucial de cet exercice est de former d'une manière ou d'une autre l'équation de la normale au point et cela c'est en principe dans les cordes d'un élève de Terminales.
Amicalement
pappus

Bonjour,
Pas forcément besoin de former l'équation de la normale.
Le point a pour coordonnées , le point   , on suppose . La droite est dirigée par le vecteur et la tangente en par . Donc est la normale à la parabole en si et seulement si

ce qui permet de construire à la règle et au compas, pourvu que .

La construction des solutions , c'est le dessin de pappus.

Bonjour à tous

Merci GBZM que je salue et que je suis heureux de retrouver ici sur un sujet aussi insignifiant pour lui.
Effectivement tous les chemins mènent à Rome et plusieurs rédactions sont possibles et les meilleures pour le bachelier d'aujourd'hui sont les plus élémentaires.
Notons que l'équation de GBZM est du second degré:

donc au programme de Terminales.
Ses racines et    vérifient:
et  
D'où ma figure supposant connue la construction géométrique de deux nombres dont on se donne la somme et le produit mais là je m'avance peut-être un peu.
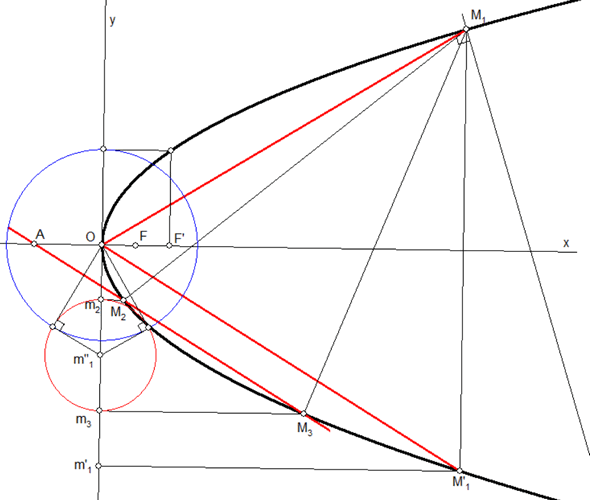
Sur ma figure, il faut lire $t=y_1$ et le point est le point de la parabole dont on cherche les normales à la parabole passant par ce point.
Le point   est le point symétrique de par rapport à l'axe.
est la projection orthogonale de sur la tangente au sommet.
est le milieu de
Le cercle bleu est le cercle de centre et de rayon .
est le symétrique de par rapport au foyer .
Le cercle rouge a pour centre   et est orthogonal au cercle bleu.
Il coupe la tangente au sommet aux points et qu'on remonte en et sur la parabole.
Suivant une de mes remarques d'un précédent message, la droite $L$ passant par les points   et a pour équation:

Elle passe par le point   et est parallèle à la droite
Le futur bachelier d'autrefois pouvait faire la figure que vous avez sous les yeux avec sa règle et son compas à l'exception du tracé de la parabole qu'il ne pouvait faire que point par point.
A la rigueur pouvait-il utiliser la courbe française si elle était permise.
Amicalement
pappus

Bonjour à tous
Je voudrais maintenant aborder la configuration  générale des normales à une parabole issues d'un point quelconque mais peut-être faut-il ouvrir une nouvelle discussion sur ce sujet d'une part parce qu'il s'éloigne trop du problème initial et d'autre part parce qu'on sort vraiment du programme de Terminales qui ne va pas plus loin que les équations du second degré en algèbre mise à part l'équation :[tex]z^2-1=0/tex] dont les racines sont celles de l'unité.
Amicalement
pappus

Bonjour pappus,
Merci pour ce sujet qui m'a bien plu. Son côté "élémentaire" m'a permis d'y mettre mon grain de sel ...

Normales à une conique (dur)

Bonjour

Oui comme on va s'éloigner...il vaut mieux ouvrir un nouveau sujet dans détente
Merci 😉