Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... LicenceMaths 2e/3e a GéométrieTopics traitant de géométrie [tout]Lister tous les topics de mathématiques
Niveau LicenceMaths 2e/3e a
Partager :

Géométrie affine

Posté par
kArMH 03-07-21 à 14:36

Bonjour,
S'il vous plaît j'ai un problème je n'ai pas compris l'énoncé du problème suivant:

Dans le plan affine euclidien, soient C_1, . . .,C_n, des cercles avec C_1 tangent à C_2 en un point I_1, . . . , C_{n-1} tangent à C_n en un point I_{n-1} et C_n tangent à C_1 en un point I_n. Pour tout point M_2 C_1 on considère le point M_2 où la droite (MI_1) recoupe le cercle C_2 (M_2 = I_1 si M_1 = I_1 ). De manière analogue, on associe à M_2 \in C_2 un point de C_3 , etc. Pour finir, on associe à M_n \in C_n le point M_0 \in C_1, où la droite (M_n I_n) recoupe C_1. Préciser la position du point M_0 par rapport à M sur le cercle C_1 .

Dans le problem : on considère le point M_2 où la droite (MI_1) recoupe le cercle C_2 . Est-ce que  M_2 est unique dans C_2 ?

Posté par
GBZMre : Géométrie affine 03-07-21 à 14:57

Bonjour,

À ton avis, si une droite coupe un cercle, combien y a-t-il de points d'intersection ?

Posté par
GBZMre : Géométrie affine 03-07-21 à 15:02

Pour ce qui est de l'exercice, essaie d'identifier la transformation du plan qui envoie M_1 sur M_2. Un dessin peu aider.
Une fois qu'on pense en termes de transformations, la réponse se voit assez clairement.

Posté par
kArMHre : Géométrie affine 03-07-21 à 15:15

Une droite coupe un cercle en deux point

Posté par
kArMHre : Géométrie affine 03-07-21 à 15:17

kArMH @ 03-07-2021 à 14:36

Bonjour,
S'il vous plaît j'ai un problème je n'ai pas compris l'énoncé du problème suivant:

Dans le plan affine euclidien, soient C_1, . . .,C_n, des cercles avec C_1 tangent à C_2 en un point I_1, . . . , C_{n-1} tangent à C_n en un point I_{n-1} et C_n tangent à C_1 en un point I_n. Pour tout point M\in C_1 on considère le point M_2 où la droite (MI_1) recoupe le cercle C_2 (M_2 = I_1 si M_1 = I_1 ). De manière analogue, on associe à M_2 \in C_2 un point de C_3 , etc. Pour finir, on associe à M_n \in C_n le point M_0 \in C_1, où la droite (M_n I_n) recoupe C_1. Préciser la position du point M_0 par rapport à M sur le cercle C_1 .

Dans le problem : on considère le point M_2 où la droite (MI_1) recoupe le cercle C_2 . Est-ce que  M_2 est unique dans C_2 ?

Posté par
kArMHre : Géométrie affine 03-07-21 à 15:24

Donc, nous avons  toujours M_2=I_1 et pour tout  i   on a M_{i+1}=I_i ?

Posté par
GBZMre : Géométrie affine 03-07-21 à 16:19

Bien sûr que non !
As-tu fait un dessin avec les deux premiers cercles C_1 et C_2 pour voir ce qui se passe ?

Posté par
verdurinre : Géométrie affine 04-07-21 à 15:44

Bonjour,
une image avec trois cercles.
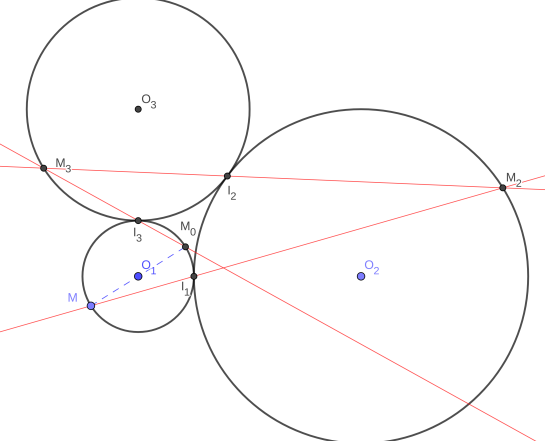
Géométrie affine
Et une remarque :
il est prudent, au moins dans un premier temps, de supposer que les points de tangence Ik sont deux à deux distincts.

Posté par
Sylvieg Moderateurre : Géométrie affine 04-07-21 à 16:44

Bonjour,
Une figure avec n = 4 :
Géométrie affine

Posté par
GBZMre : Géométrie affine 04-07-21 à 17:58

Bonne fin de week-end !

Et pour mettre un peu de variété, vous pouvez aller voir ici :

Posté par
Sylvieg Moderateurre : Géométrie affine 04-07-21 à 18:23

Joli !
Bonne fin de week-end à toi aussi GBZM

Posté par
GBZMre : Géométrie affine 04-07-21 à 18:26

Tout ça devrait permettre à kArMH de répondre à ma question : quelle est la transformation affine qui fait passer de M_1 à M_2 ? Une fois ceci vu, ça coule presque tout seul.

Posté par
Sylvieg Moderateurre : Géométrie affine 20-07-21 à 12:26

Bonjour,
Plus de deux semaines ont passé.
Pour ceux qui pourraient être intéressés, je propose une aide sous forme de deux figures :
Géométrie affine

Géométrie affine


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1675 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !