Inscription / Connexion Nouveau Sujet
géométrie descriptive
bonjour pourriez vous m'aider pour cet exercice merci de votre aide
un plan P est donné par ses traces P  Q'
Q'
1) rabattre le plan P sur le plan horizontal de projection . Déterminer le rabattement de la trace frontale. En déduire le rabattement d'un point quelconque M du plan P
2)on désigne par  et
et  les angles respectifs des deux traces avec la ligne de terre OY. D'autre part, on désigne par
les angles respectifs des deux traces avec la ligne de terre OY. D'autre part, on désigne par  l'angle que font entre elles les deux traces dans le plan P. En utilisant la construction du 1° , exprimer cos
l'angle que font entre elles les deux traces dans le plan P. En utilisant la construction du 1° , exprimer cos  en fonction de
en fonction de  et
et 
3) un plan T a même trace horizontale que la plan P. un triangle équilatéral de 6 cm de côté est situé dans ce plan T. un de ces sommets est en  , les deux autres sommets R et S étant respectivement sur les traces du plan T. construire les deux projections de ce triangle.
, les deux autres sommets R et S étant respectivement sur les traces du plan T. construire les deux projections de ce triangle.
Bonjour,
Je crois que c' est le dernier de la série 
D' abord, une épure:
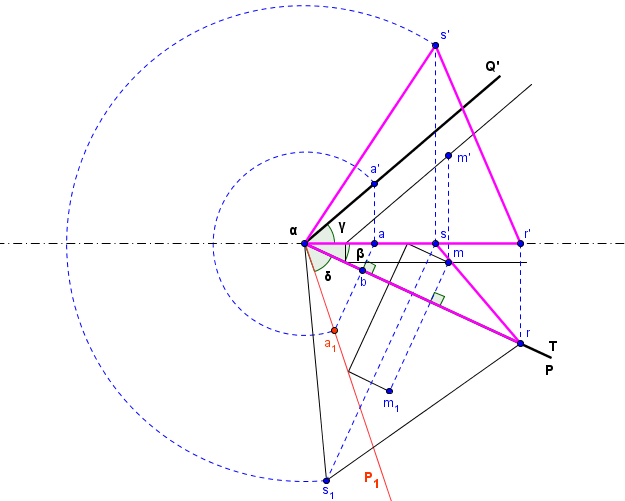
1)La trace frontale est rabattue en à l' aide d' un point
quelconque de cette trace frontale.
Le segment se projette en vraie grandeur en
Ce segment conservant sa longueur dans le rabattement, on a et
est sur la perpendiculaire abaissée de
sur la charnière
2)
3) On trace le triangle équilatéral dans le plan horizontal.
On le relève ensuite en



 géométrie en post-bac
géométrie en post-bac