Inscription / Connexion Nouveau Sujet
Géométrie...impasse!
modération > **Bonjour***
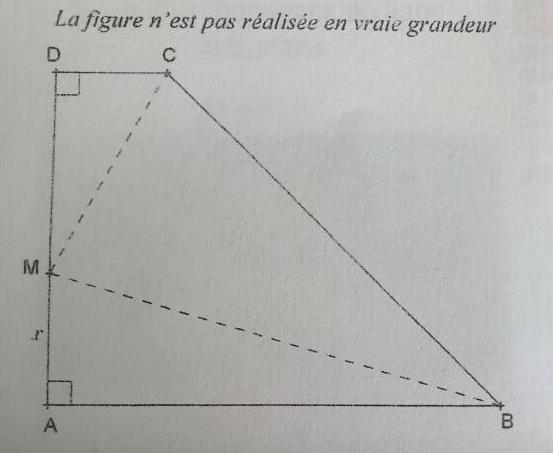
Abcd est un trapeze rectangle en A et d avec ab=8 ad=6 et dc=2.
Le point M se déplace sur le segment AD
On note AM=x
Existe t'il une position de M sur AD telle que les aires des 3 triangles AMB, MDC,MCB soient égales?
Bonjour, si quelqu'un peux au moins me donner une piste pour demarrer...je bloque!
Merci d'avance
Merci pour votre réponse;
J'ai calculé l'aire du trapère, celle des 2 triangles rectangles et j'ai soustrait ces 2 aires de l'aire du trapèze pour obtenir l'aire du 3ieme triangle qui n'est pas rectangle. La difficulté, c'est de faire varier le point M sur AD pour obtenir eventuellement 3 triangles de surface égale. C'est là que je bloque...
Bonjour,
juste en passant (carpediem continuera)
si tu n'écris pas ici ce que tu as trouvé on ne peut pas
- vérifier que c'est juste
- t'aider à conclure
Bonjour et de passage aussi
Si tu as calculé l'aire des trois triangles, tu les as en fonction de x.
Donne nous leur valeur respective, puis traduit par une équation l'égalité de leur aire.
encore un exo abandonné par flemme de recopier un résultat de 3 lignes ...
et puis bien lire l'énoncé :
Existe t'il ...
la réponse peut très bien être "non, il n'en existe pas"
méthode quasiment sans calcul (mais réduisant à néant le but de l'exo : s'exercer au calcul littéral et aux équations) :
si les aires sont égales, c'est que chacune d'elles est le 1/3 de l'aire du trapèze
on peut alors facilement placer M pour que l'aire de AMB soit égale à ça.
puis calculer (désormais en valeur numérique !) les aires des deux autres ...
merci pour vos conseils: j'ai donc calculé l'aire du trapèze DCAB, S=(DC+AB)CC'/2 ou CC4 est la hauteur=6.on obtient S=30. donc on cherche a savoir si il existe M appartenant a AD tel que l'aire de MDC(T1)=aire de MAB(T2)=aire de MCB(T3)=1/3S=10.
aire T1, T1 rectangle en D:1/2DC*DM=10 ou DM=10 et DM=kAM=kx=10
aire T2, T2 rectangle en A:1/2MA*AB=10 donc 1/2x*8=10 , x=5/2. Donc pour AT2=10 il faut AM=x=5/2. si on reporte la valeurdans la formule de calcul de l'AT1 M=kAM=kx ou k=4 et x=5/2 on obtient DM=10. donc il n'existe pas M appartenant à DA telle que AT1=AT2=AT3. merci de me dire si cela vous parait correcte.
M=kAM=kx ou k=4 et x=5/2 on obtient DM=10. donc il n'existe pas M appartenant à DA telle que AT1=AT2=AT3. merci de me dire si cela vous parait correcte.
certes mais inutilement compliqué ... que vient faire ce "k" ici ?
aire de MAB = 10 donne directement AM
donc DM directement (AD - AM) et donc aire de MCD directement et conclusion directe.
mais ce qui est très certainement attendu est plutôt de faire un calcul littéral et des équations !
"en fonction de l'inconnue x" définie dans l'énoncé (sinon on n'en aurait rien dit dans cet énoncé)
aire de MAB = 1/2 AB.AM = 4x
MD = AD - AM = 6-x
donc aire de MCD = ... en fonction de x
idem pour MBC en fonction de x
c'est ces formules là qu'on attendait depuis 2 jours....
que tu prétendais avoir obtenues, le 11-04-22 à 11:29, et que tu refusais de donner, à moins que tu ne les aies pas obtenues du tout, et dans ce cas on se demandait bien ce que tu avais calculé ("on ne peut pas vérifier que c'est juste")
et ensuite les aires égales donnent des équations en l'inconnue x
aire MAB = aire MCD
et aire MAB = aire MBC
qui s'avèrent incompatibles, d'où la conclusion
bonjour, je vous remercie beaucoup pour vos explications. cet exercice est pour le 19/4 et j'ai cherché la solution ce week end mais je me suis effectivement compliqué la vie en cherchant a exprimer dm en fonction de am ...d'ou le k. et je me retrouvais avec des equations qui contenais 2 inconnues d'ou le blocage.
Sinon je me suis inscris lundi sur le site et c'est ma première utilisation, donc je m'excuse pour les retards de réponse, d'autant que je ne suis pas encore en vacances et que j'ai toujours cours, et que j'ai refait les raisonnements et les calculs plusieurs fois (en particulier pour essayer de supprimer ce k qui m'embetait bien). D'autre part je n'avais pas formuler correctement le fait que si les 3 triangles avaient la meme aire celle cie était égale à 1/3 de l'aire du trapèze...ce qui me faisait une inconnue supplémentaire. j'avais bien calculé depuis le début l'aire du trapèze mais ensuite je calculais séparement les aires des triangles c'était trop compliqué. en tous les cas merci beaucoup pour votre patience vos conseils ;j 'ai bien compris la solution.
certes ... mais bon ...
comme l'a dit mathafou avec l'unique variable x on peut calculer l'aire du trapèze et des trois triangles uniquement en fonction de x ...
pour résoudre deux équations qui donneront des résultats contradictoires donc pas de solution !!
et c'est ce qui est très certainement demandé ici
ici tu as recopié un raisonnement que tu n'as pas trouvé !!!
DM en fonction de AM c'est juste DM = AD - AM ... ( = 6 - x vu que AD c'est 6 et AM c'est x)
nul besoin d'introduire des inconnues supplémentaires

pour résoudre on peut :
soit écrire sans se poser de question que les aires sont égales entre elles :
aire MAB = aire MCD = aire MBC
ça fait 2 équations indépendantes :
aire MAB = aire MCD, et aire MAB = aire MBC
qui doivent donner la même solution (et même dans [0; 6] vu que M est un point du segment [AD])
et tout ça en fonction de la seule inconnue x
soit écrire qu'elles sont égales chacune au 1/3 de l'aire du trapèze :
aire MAB = 10
et aire MCD = 10
encore une fois en fonction de la seule inconnue x
qui doivent là aussi donner la même solution et dans [0; 6]
Pour les retards de réponse, OK.
je comprends que en fait tu ne peux te connecter que pendant la pause de midi ...
"mais ensuite je calculais séparément..." on aurait pu voir ça et t'orienter correctement si tu avais donné tes calculs et tes essais dès le départ
(règles générale du forum ![]() A LIRE AVANT DE POSTER OU DE RÉPONDRE, MERCI : "... et ses recherches ..." )
A LIRE AVANT DE POSTER OU DE RÉPONDRE, MERCI : "... et ses recherches ..." )