Inscription / Connexion Nouveau Sujet
Géométrie projeté orthogonal
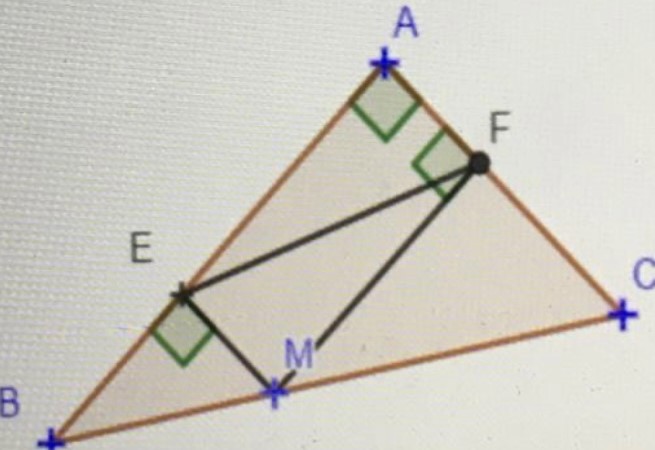
Bonjour ! j'aurais besoin d'aide pour cet exercice s'il vous plait soit ABC un triangle rectangle en A.
Soit M un point du segment [BC], E le projeté orthogonal de M sur (AB) et F le projeté orthogonal de M sur (AC)
1. Déterminer la nature du quadrilatère MEAF.
2. En déduire la position de M sur [BC] pour laquelle la longueur EF est minimale.
Merci d'avance !
Pour l'instant pour le premier j'ai constaté que c'était un rectangle car il a 4 angles droits, et pour la position du point M sur BC je dirais qu'elle doit être équidistant de la longueur EF donc placer à une position où M est équidistant de BC et EF ? Moi je suis vraiment pas sûr
Pourquoi avoir commencé à créer un autre compte ?
Ameliadespi34 est à supprimer si tu veux continuer à avoir de l'aide.
Mais c'est étrange que vous voyez mon compte '' Ameliadespi34'' alors que ce compte quand j'essaye de la supprimer on me dit que ce compte n'a pas encore été validé
Je ne me suis pas rendu à l'URL indiquée dans le mail donc puisque le compte n'est pas validé il sera automatiquement supprimé au bout de quelques jours
D'accord 
Pour l'exercice :
Quelles propriétés connais-tu pour le rectangle ?
Essaye de sélectionner celle qui peut être utile pour la longueur EF.
La propriété que je connais pour le rectangle c'est qu'il a des diagonales qui ont le même milieu et qui sont de même longueur
Donc M il est déjà placé du coup sur mon schéma, pour connaître où se situe M il faut tracer la droite AM
Et j'ai une question si on veut rendre la longueur EF minimale alors cela vient aussi à rendre minimale la distance AM puisque ce sont deux diagonales de même longueur c'est ça ?
Merci infiniment pour votre aide, votre aide m'a beaucoup servi ! Pour être sûr d'avoir compris cette histoire de longueur minimale, si on nomme le point H un point du segment BC, et il faut que AM soit minimale, alors le point H sera placé à la même place que E ?
Je ne comprends pas bien ton dernier message.
Avec H sur [BC], il aura un peu de mal à être en E qui est sur un autre côté du triangle.
Utilise une autre figure avec une droite (BC), un point A extérieur à cette droite.
Comment placer M sur (BC) pour que la longueur AM soit la plus petite possible ?
Ce point se nomme le projeté orthogonal H de A sur la droite BC ? Et pour le construire on trace une droite passant par AM et perpendiculaire à BC ?
une droite passant par AM le point A et perpendiculaire à BC ?
Oui, et cette droite porte aussi un nom dans le triangle ABC.
Bonjour
Mais si on devrait placer le point H pour que AM soit minimal
H est le pied de la hauteur issue de A, il ne dépend pas de M ni d'aucune condition sur M, E ou F
la réponse de Sylvieg "au même endroit" est à mettre en face de sa réponse précédente
(H est tout de même à la même place que M est faux )
C'est plutôt M qui doit être à la place de H
et en mettant les poins sur les I :
EF = AM ; donc M au même endroit. (= aussi en H)
avec une autre condition que "EF minimum" il faudrait mettre M peut être ailleurs que en H , H étant toujours H défini comme pied de la hauteur quoi qu'il arrive
par exemple : où faut il mettre M pour que EF = 1/2 BC ?
réponse (je ne te demande pas de le démontrer) :
M en I, milieu de [BC] ou en J, symétrique de I par rapport à H (si ce point J est dans le segment [BC])
version animée (on peut déplacer M)