- Un petit rappel de Cours sur le dénombrement - terminale
- Sept Exercices Q.C.M. sur le dénombrement - terminale
- Complexes, calcul vectoriel, problème - sujet de bac - terminale
- Enseignement scientifique : suite, probabilité, fonction - sujet de bac - terminale
- Enseignement scientifique : suite, probabilité, fonction - sujet de bac - terminale
Inscription / Connexion Nouveau Sujet
Grand Oral maths_equa diff et modèles
Bonjour,
J'ai trouvé une question intéressante pour le grand oral, mais je ne sais pas encore comment l'introduire.
Les équations différentielles permettent-elles de modéliser l'évolution temporelle d'un système ?
C'est une transversale entre les mathématiques et la physique-chimie.
Mon problème est que les deux enseignants qui assisteront à mon oral ne font pas forcement partis de ses deux spécialités. Je ne veux donc pas partir trop dans les détails durant les 5 premières minutes par peur de perdre un membre du jury qui ne comprenne rien à ce que je suis en train de lui raconter.
salut
la question tournée ainsi semble guère intéressante vu que c'est évidemment oui !!
je verrai plutôt la même question mais commençant par comment ou en quoi
...
et il n'est pas nécessaire de rentrer dans les détails durant le premier temps ...
choisir deux exemples "élémentaires" ou un exemple "élémentaire" et un "plus compliqué" mais "théorique" qui pourront être (un peu) développé dans le second temps ...
pour deux exemples "classiques" :
chute d'un corps
mouvement d'une particule dans un champ électromagnétique
... entre autres ...
d'accord d'accord.
Mais je ne vois pas comment introduire le sujet sans que ce soit trop compliqué a comprendre.
Je ne veux pas partir directement sur l'explication de la notion d'equation différentielle.
tu n'as pas à t'occuper de savoir si c'est trop compliqué et si le jury comprend ou ne comprend pas !!
l'important c'est que toi tu comprennes et que tu saches répondre à toutes les questions qui puissent t'être posées ensuite !!
de toute façon en 5 mn tu dois exposer brièvement un ou deux exemples mettant en œuvre des équa dif permettant de modéliser/solutionner un pb ...
En quoi les équations différentielles permettent-elles de modéliser l'évolution temporelle d'un système ?
Voici donc mon introduction et le debut de mon développement:
L'équation différentielle est un objet sur lequel l'apprenant est amené à travailler au niveau de la recherche de solutions. La résolution des équations différentielles peut être abordée à l'aide de trois approches : l'approche algébrique, l'approche numérique et l'approche qualitative.
Résumons, sans entrer dans les détails, le fonctionnement de chacune de ces approches.
Les méthodes algébriques de résolution d'équations différentielles sont les plus connues et les plus répandues depuis leur apparition dans le monde des mathématiques. Ces méthodes donnent des solutions exactes sous la forme des formules explicites, d'expressions finies, de développements en séries ou d'expressions intégrales. Cependant ces méthodes ne sont pas suffisantes pour résoudre tous les types d'équations différentielles ; il existe, en effet, plusieurs types d'équations différentielles et chacun d'eux implique une méthode de résolution particulière.
Cette insuffisance nécessite l'intervention de nouvelles méthodes : les méthodes numériques et graphiques. Les méthodes numériques permettent presque toujours d'approximer la solution d'une équation donnée vérifiant une condition initiale donnée. Il existe plusieurs de ces méthodes, dont les plus connues sont la méthode d'Euler et la méthode de Runge-Kutta .
Pour résoudre une équation différentielle d'ordre peu élevé, on peut utiliser aussi une construction graphique. La méthode graphique de base est celle des isoclines. Elle s'applique directement aux « équations du premier ordre que l'on peut écrire sous la forme : y'(x) = f(x, y) (E). Une fonction y est la solution de (E) si en tout point (x, y(x)), la tangente à la courbe représentative a pour pente f(x, y(x)). On peut alors calculer, pour tout point du plan, la valeur numÈrique de f(x, y(x)) ce qui permet la construction de la courbe. Cette méthode donne rapidement un aperçu du comportement des solutions, et plus précisément de leurs comportements à long terme.
4.2. Modèle "équation différentielle"
Dans le domaine de la physique, notre objet d'étude (les équations différentielles) est considéré en tant que modèle utilisable pour décrire les phénomènes étudiés, expliquer leurs relations et prévoir leur évolution.
Qu'est ce que vous en pensez ?
(Par la suite je parlerais de plusieurs systèmes qu'on a vu cette année en physique-chimie)
Merci d'avance.
je dirai que c'est pas mal ou du moins intéressant ... et je n'en dirai pas plus ...
mais tu peux aller voir tes prof pour en discuter avec eux ...
Bonsoir,
Je viens de finir ma question du grand oral.
Je l'ai donc reformulée:
En quoi les équations différentielles permettent de modéliser l'évolution temporelle d'un système ?
Je suis donc en train d'apprendre la première partie qui dure 5 minutes dont voici ci-joint le contenu.
Je m'interroge désormais sur la deuxième partie du Grand Oral.
Je me demandes quelles questions peuvent me poser les jurys concernant le contenu de ma question.
Je voudrais donc savoir, vous, quelles questions vous poseriez en lisant le contenu de ma question ?
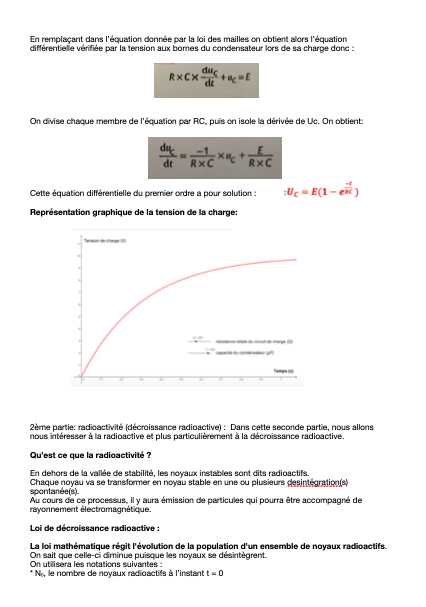
Je me demandes aussi si le temps sera assez suffisant pour présenter les deux démonstrations (charge d'un condensateur et loi de décroissance radioactive) ?
Merci d'avance,
Cordialement. 
PDF - 240 Ko
Bonjour
Une équation différentielle est une équation où l'inconnue est une fonction, et qui se présente sous la forme d'une relation entre cette fonction et ses dérivées.
Tu peux donner un exemple.
J'apprécie tout particulièrement les équations différentielles car c'est un raisonnement méthodique et intéressant.
Ah bon ?
Pour ma part, j'aurais écrit par exemple pour un premier jet : mon appétence pour les équations différentielles provient du fait indéniable de leur impact sur la quasi-totalité des sciences, y compris les sciences économiques. Leurs résolutions font appel soit à des techniques théoriques, soit le plus souvent à des techniques numériques.
En relisant, je remarque qu'il y a des choses à modifier. Je te laisse travailler.
Ton illustration concerne une équation différentielle du premier ordre et à coefficients constants, qui se résout théoriquement.
Peut-être serait-il approprié de donner l'exemple d'une ED qui se résout uniquement numériquement.
Pour le reste; tu ne peux pas te contenter de faire du copier-coller. A la rigueur, tu peux te servir des schémas au moyen d'un outil de rognage.
D'accord merci pour votre réponse.
Je vais modifié ce que vous m'avez dit de modifier.
Néanmoins, vous me parlez de copier/coller alors que je ne l'ai que fait pour sur le cours et la démonstration à proprement dit.
Après je ne vais pas dire tout ce que j'ai mis dans la leçon car il y a des choses supplémentaires qui me permette d'en savoir davantage sur le sujet.
Ensuite, je penses que j'enlèverais seulement les sciences économiques dont vous me parlez ci-dessus car je n'ai pas fait de S.E.S durant cette année mais de la physique-chimie et des mathématiques.
Apres quand vous parlez de méthodes de résolution numérique, pouvez-vous me donner un exemple car je ne sais pas si je l'ai vu en cours ?
Merci encore pour votre aide qui m'est chère,
Cordialement.
En tant que lycéen qui a déjà passe l'épreuve du grand oral, je pense que tout d'abord c'est un peu trop grand, les 5 min passent très vite. Personnellement, je conseillerais de ne pas dépasser la barre des 900 mots, c'est vraiment le maximum.
D'autre part, il faut se rappeler que tu ne pourras pas utiliser un tableau lors de ton épreuve, il est donc un peu difficile de faire comprendre au jury les calculs que tu fais. J'ai l'impression qu'ils s'attendent a une approche (presque) totalement théorique.. Encore ce n'est qu'une impression mais dans un exemple d'exposé de grand oral que j'ai dans un des prépa-bac, il n y avait (presque) pas de calcul..
D'accord, je pense enlever toutes les étapes intermédiaires permettant d'obtenir les résultats final. (ces étapes intermédiaires je pourrais les expliquer lors de la second partie sur le tableau si ils me le demandes bien sur).
De plus, en re-faisant dans ma tête et à l'oral, je me suis apercu comme vu que c'était trop long.
Donc je pense que je ne ferais simplement pas la 2ème partie.
Je pense que c'est suffisant et si jamais il veulent davantage d'exemple, je leur expliciterais pendant la 2ème partie.
Comme ça fera 4 relations avec le circuit électrique, le schéma d'un condensateur et la représentation graphique que je re-transcrirais sur ma feuille pendant les 20 minutes de préparation.
Cela vous convient ?
Salut frero, alors tout c'est bien passé pour ton sujet ? Les équations différentielles sont une branches tellement intéressant
Salut tout s'est bien passé lors de mon oral . J'ai eu 18/20 mais je ne suis pas passé sur ce sujet mais il reste intéressant à aborder.
Re,
Ta deja passé le Grand Oral ou ce n'était que le blanc ?
C'est quoi ton sujet de physique du coup ?
J'ai effectivement déjà passé le grand oral officiellement.
Si je peux te donner un conseil, bosse tes deux questions autant l'une que l'autre et ne joue pas aux probabilités. En plus, tu ne connais pas la composition du jury. Mon jury était composé d'une professeur d'espagnol et d'un professeur de mathématique et il se trouve que je suis passé sur le sujet de Physique-Chimie.
En Physique-Chimie, j'ai abordé le contrôle qualité du chocolat par la diffraction des grains d'une poudre de cacao.