Inscription / Connexion Nouveau Sujet
Bonjour Lake,oui je reprends un peu la descriptive entre deux conceptions. Tout d'abord j'ai dessiné la projection horizontale. J'ai reporté 8 génitrices sur la spirale sachant que la longueur de la première est de 500 mm (celle de couleur rouge qui serait en V.G sur la projection frontale, JE pense ,la deuxième (en vert )de 1000 mm, la troisième (en jaune) de 1500, etc. Elles sont ensuite projetées sur la ligne de terre de la projection frontale, et recoupées suivant le deuxième cylindre.
En y regardant de plus près (avec une loupe  ) l'hélice bleue, c'est à dire l'hélice intersection de l'hélicoïde avec le cylindre extérieur, a une allure bizarre.
) l'hélice bleue, c'est à dire l'hélice intersection de l'hélicoïde avec le cylindre extérieur, a une allure bizarre.
Ce n'est pas trop étonnant, les génératrices de l'hélicoïde ne sont pas tangentes à l'hélice directrice. Regarde les jaune, violettes et vertes de la projection frontale.
Tu n'as pas le choix: pour faire une construction correcte, il faut procéder pas à pas comme je te l'avais indiqué ici ( est tangente en
à l'hélice directrice noire en projection frontale) :
En premier lieu, une épure d' un hélicoïde développable:
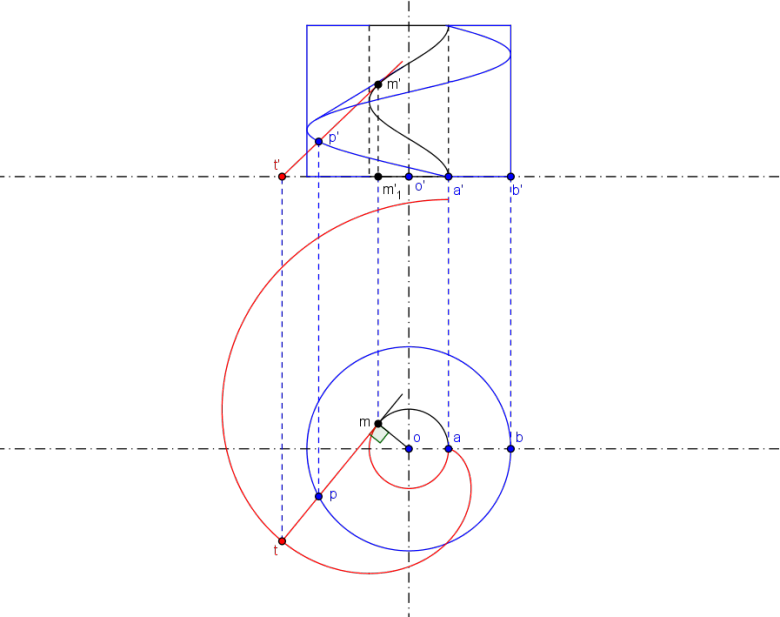
On commence par l' hélice sur le cylindre intérieur (l' hélice directrice):
La cote du point courant
donc on reporte sur la ligne de rappel de
On construit ensuite la tangente à cette hélice
En projection horizontale, cette tangente est tangente en
On reporte
Lorsque
Reste à couper l' hélicoïde par un cylindre extérieur pour le visualiser (en bleu); on obtient une seconde hélice de point courant

Bonjour Lake,
J'ai essayé d'inséré l'image dans mon logiciel afin de reproduire ton épure, j'ai une fonction « tangente », curieusement les génératrices mes ne correspondent pas du tout avec les tiennes...!
Le cercle de la base du cylindre est subdivisé en combien de partis égales s'il te plait, un angle de départ particulier ?
Dans l'attente,
La solution, ça serait peut-être que je le modélise en 3 dimensions et de fractionné l'écran en 2 vues (projection frontale et horizontale)…
Sur mon épure au dessus, il n'y a qu'une génératrice de tracée: .
Et bien sûr, il faut utiliser simultanément les deux projections (horizontale et frontale) pour effectuer les constructions.
L'ordre des choses:
1) Il faut construire l'hélice directrice: la projection horizontale est le petit cercle; la projection frontale est la courbe noire.
2) On choisit un point quelconque sur la projection horizontale de cette hélice (qui est le petit cercle).
3) Avec une ligne de rappel, on obtient en projection frontale sur la projection frontale (noire) de l'hélice directrice.
4) En projection horizontale, sur la perpendiculaire à passant par
, on reporte à partir de
la longueur de l'arc
(rouge) on obtient le point
:
5) Avec une ligne de rappel à partir de , on construit
sur la ligne de terre.
Si la construction est correcte, en projection frontale, la droite (rouge) est automatiquement tangente en
à la projection frontale de l'hélice directrice (noire).
6) Le cylindre extérieur étant donné, en projection horizontale, la droite recoupe le cercle projection de ce cylindre en
.
7) La ligne de rappel issue de recoupe
en
On a ainsi obtenu le point , intersection de la génératrice
de l'hélicoïde avec le cylindre extérieur.
Pour avoir d'autres génératrices/intersections, on choisit d'autres points quelconques en projection horizontale sur le petit cercle et on recommence l'opération pour chacun de ces points.
En joignant les points correspondants , on obtient la développante de cercle (l'espèce de spirale) en projection horizontale.
En joignant les points correspondants , on obtient la projection frontale de l'intersection hélicoïde/cylindre extérieur: l'hélice en bleu de même pas que l'hélice directrice.
Avec le logiciel que j'utilise (GeoGebra), j'ai une fonction "lieu" qui permet de tracer les lieux des points et
lorsque
décrit le cercle projection horizontale du petit cylindre. Je n'ai pas besoin de "joindre" les différents points; le logiciel le fait pour moi.
Encore une fois, il faut que tu mènes de front les diverses constructions sur les deux vues, frontale et horizontale. Sinon, rien ne marchera...

Bonjour Lake et encore merci pour ton temps.
JE PENSE AVOIR ENFIN COMPRIS COMMENT CONSTRUIRE EN PROJECTION HORIZONTALE (m,t).Effectivement en projection frontale (m',t' )en bien tangente en point (m') à l'hélice directrice !
Comment fais-tu pour terminer l'hélicoïde s'il te plait, pour la parti supérieur(voir capture d'écran et aussi voir aussi si la deuxième génératrice rouge est bien placée (génératrice rouge à droite de l'épure en projection horizontale).
Bonsoir david1972,
Jusqu'à 21h29, tout va bien. Mais à 21h32, ta seconde génératrice rouge est fausse: en projection horizontale, tu l'as orientée vers le Sud sud Est alors qu' il faut l'orienter vers le Nord nord Ouest (à l'opposé).
Regarde tes autres génératrices: elles "tournent" autour du petit cylindre sans changer de sens. Seule la dernière (rouge) a changé d'orientation. En l'orientant correctement en projection horizontale, tu pourras aussi prolonger la "spirale".

Au fait:
JE PENSE AVOIR ENFIN COMPRIS COMMENT CONSTRUIRE EN PROJECTION HORIZONTALE (m,t).Effectivement en projection frontale (m',t' ) est bien tangente au point (m') à l'hélice directrice !
Je crois aussi que tu y es!

Il y a quelque chose qui ne va pas à 00h1 et c'est un peu de ma faute: j'avais éludé le problème en pensant: "on a le temps..." Ta réaction a été plus rapide que prévu et prouve que tu as bien suivi la construction:
Comment fais-tu pour terminer l'hélicoïde s'il te plait, pour la parti supérieure
Tu as raison, il y a un problème:
Les génératrices
En projection frontale (épure de 11h09), le point
Mais quand le point
Autrement dit, sur ton dessin de 00h11, les tangentes en projection horizontale (et donc les tangentes tout court) à l'hélice directrice ne sont correctes que jusqu' à la tangente verte "verticale". Les suivantes sont fausses.
On peut tout de même avoir une construction pour la suite en prolongeant l'hélice directrice vers "le haut":
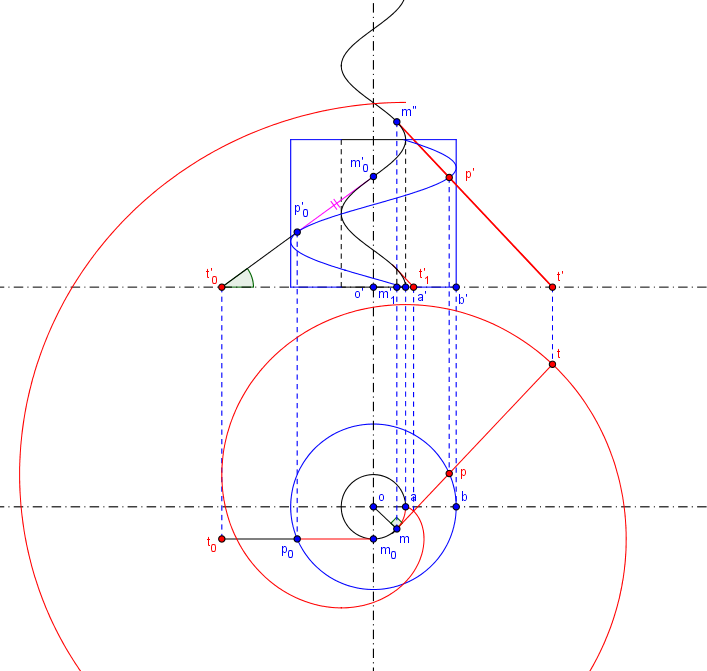
Le point
La longueur reportée
Pour le reste, la construction reste la même.
Je reviens sur le développement plus tard...

Le développement:
On obtient (je crois que tu l'as vu) la vraie grandeur d'une tangente limitée par les deux cylindres en sur la projection frontale. On obtient en vraie grandeur par la même occasion l'angle
(constant: voir la perspective en page précédente de ce topic) que font les tangentes avec un plan horizontal.
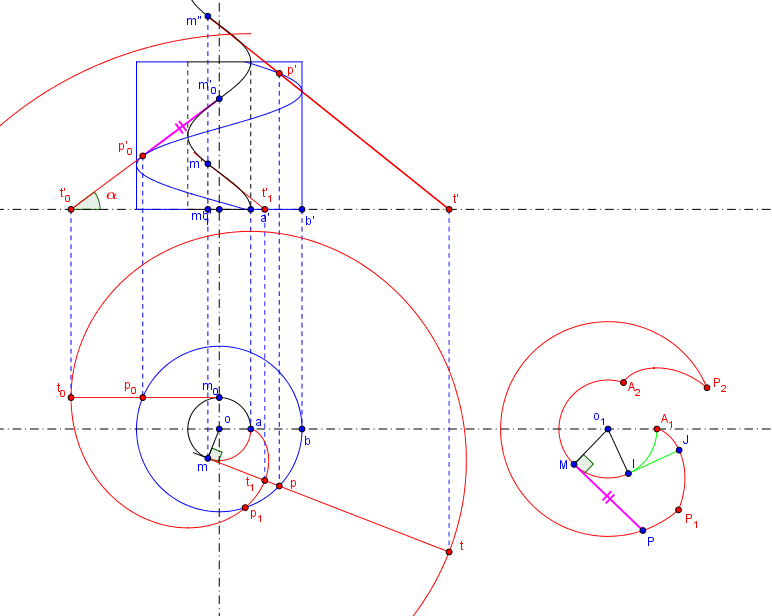
On passe au développement:
Je te demande d'admettre que le cercle intérieur du développement a pour rayon où
est le rayon réel du petit cylindre.
L'hélice directrice à une longueur sur un pas de
(retourne à la perspective où on a
avec Pythagore,
représentant la longueur de l'hélice sur un pas).
On reporte cette longueur sur le développement à partir de (dans le sens des aiguilles d'une montre) pour obtenir
en sorte que l'arc
soit égal à cette longueur.
A partir d'un point quelconque de cet arc, on reporte sur la tangente à l'arc la vraie grandeur d'une génératrice limitée par les deux cylindres
pour obtenir un point
Le cercle de centre passant par
limite le développement extérieurement.
Reste à voir ce qui se passe à proximité des points et
:
En projection horizontale, les tangentes à l'hélice directrice, en début de parcours du point sur cette hélice, coupent le plan horizontal de projection avant de couper le cylindre extérieur. Il y en a une de dessinée en
où
est la trace de cette tangente sur le plan horizontal de projection.
La trajectoire du pied de cette tangente, qui correspond à l'arc plan d'une développante de cercle, est défini par mt_1=
.
Cette courbe est la section de l'hélicoïde par le plan horizontal de projection.
Lorsque cette trace atteint , le pied de la tangente atteint le cylindre et commence son ascension sur ce même cylindre en décrivant l'hélice bleue.
Ce point limite se retrouve en
sur le développement ainsi qu'une autre développante de cercle de
à
définie par IJ=
Le même phénomène se retrouve au sommet de l'hélicoïde: sa section par le plan horizontal de cote (le pas de l'hélice) et détermine une nouvelle développante de cercle de
à
Peut-être un peu indigeste mais je ne vois guère comment t'expliquer ça autrement...

Bon,ça te parait correct?Comment mesures-tu l'éloignement de( ij) sur la projection frontale ?
Au fait,tu bosses sur un logiciel CAO ou uniquement en deux dimensions?Connais-tu un bon ouvrage de géométrie descriptique?
Cordialement.
Je pense effectivement que ton épure est correcte. Si je peux me permettre, elle a un petit défaut:
Ton hélice rose en projection frontale est un peu biscornue. Je crois en connaître la cause. Tu la traces point par point et je suppose qu'il y a une phase manuelle dans le raccordement de ces points. Tu n'y peux pas grand chose...
Au sujet de ma propre figure: le développement en bas à droite est totalement indépendant des projections frontale et horizontale (sauf pour le rayon du cylindre intérieur qui vaut , la longueur de la génératrice
et le placement du point
)
J'ai juste placé une des génératrices (quelconque) qui coupe le plan horizontal de projection (au point ) en
au même titre que
qui elle est une génératrice "normale" qui coupe le cylindre extérieur avant de rencontrer le plan horizontal de projection.
Pour les dessins, j'utilise GeoGebra qui n'est pas du tout un logiciel de CAO. Il me permet de faire des constructions (droites, cercles, intersections de ces éléments, lieux de points dépendant d'un autre point...) En fait, je fais avec ce logiciel des épures de descriptive comme je le ferais avec une planche à dessin (avec les projections sur deux plans).
L'avantage (que tu n'as peut-être pas) est que si je modifie un élément (par exemple ici le diamètre d'un cylindre ou le pas de l'hélice), tous les autres éléments du dessin suivent le mouvement. C'est un logiciel de géométrie "dynamique".
L'inconvénient est que je suis obligé de cacher les traits de construction pour que le dessin soit lisible. Tu n'imagines pas la complexité réelle d'un dessin tel que celui posté au dessus. Si tu y tiens je peux te montrer le dessin complet (c'est très moche...)
Quant aux bouquins, oui, j'ai quelques références:
- Traité de Géométrie descriptive. C.Roubaudi chez Masson.
Pour moi, la bible. Mais c'est un bouquin de haut niveau. Il était destiné aux élèves de Math Spé. Il date de 1946. On le trouve encore d'occasion à des prix raisonnables sur Price Minister ou autres.
- Géométrie descriptive. J. Avignant chez Dunod.
Un très bon bouquin d'un niveau moins élevé que le précédent.
C'est dans ce bouquin que j'ai tiré toutes les informations relatives à l'hélicoïde développable dont je n'avais jamais entendu parler avant ton intervention.
Il date de 1975. Tu peux aussi le trouver d'occasion.
En livre récent, il n'y a pas grand chose si ce n'est:
Géométrie descriptive. Du point aux surfaces de révolution et aux ombres. Alain Faure chez Ellipses.
Je l'ai et .... je ne l'aime pas.

Quant à moi j'utilise un ouvrage(que ma confié mon père) de tracés, dédié au métier de la chaudronnerie, métier qu'il a exercé.Apparement c'est d'un niveau allant du CAP ou BEI???Je ne sais pas à quoi correspond ce diplôme. J'ai aussi "traité d'ébénisterie "de Lucien Chanson, conseillé par mon ancien formateur à l'IEF-CTF de Mouchard dans le Jura.
Et voilà l',hélicoide sur 360°,simplement je te laisse regardé le rendu de son développement,ça me parait bizarre,je pensais entres autres limiter la surface par 2 cercles et ce n'est pas le cas,c'est sans doute dû à la déformation...
Bonsoir,
A vue de nez, ça ne me parait pas mal; je ne sais pas comment fonctionne ton logiciel mais en principe, si l'hélicoïde est limité par deux cylindres coaxiaux, le développement doit être limité par deux cercles concentriques. Personnellement, je n'ai pas les moyens de dessiner une perspective...
Je préfère les regarder:

L'intrados de l'escalier du Louvre est un hélicoïde développable (l'escalier lui même étant un hélicoïde droit) 
On distingue même au sol la section de l'hélicoïde par le plan horizontal: une développante de cercle! 
Une méridienne ne se définit que pour une surface de révolution. C'est l'intersection de cette surface par un plan contenant son axe. L'hélicoïde n'est pas une surface de révolution. Donc pas de méridienne pour lui.
Pour en finir avec l'hélicoïde développable, deux remarques:
1)
... le rendu de son développement,ça me parait bizarre,je pensais entres autres limiter la surface par 2 cercles et ce n'est pas le cas,c'est sans doute dû à la déformation...
Je pense que ta construction de l'hélicoïde (la perspective de 20h53) est juste bien que je n'ai aucun moyen de le vérifier.
Par contre, je pense aussi que ton logiciel construit automatiquement un développement à partir des données 3D que tu lui a fournies. Tu n'interviens plus si ce n'est pour appuyer sur une commande "développement".Et en l'occurrence, ton logiciel fait un développement approché. C'est à dire de mon point de vue un développement faux. Ce qui explique tes arcs qui ne sont pas des arcs de cercles.
2) La deuxième hélice de même pas que l'hélice directrice est la trace de la génératrice sur le cylindre extérieur. Je n'en ai pas parlé parce que les dessins (et les constructions qui vont avec) sont suffisamment compliqués, mais une génératrice est une droite. J'ai fait le choix de ne tenir compte que de sa partie "inférieure" à partir du point de contact
Autrement dit, l'intersection de l'hélicoïde développable et du cylindre extérieur est constituée de deux hélices.

Bonjour Lake, oui en effet je n'ai pas réussi à "lisser toutes les génératrices pour créer des portion d'hélicoïde droites développables il à donc fallu faire un lissage normal d'où sans doute cette déformation ou une erreur de ma part sur la répartitions des génératrices .L'idéal en effet c'est de lisser ou d'unir deux hélice comme je la fais sur l'escalier de ce matin. Concernant la méridienne je joins une petite capture d'écran.
Bonne soirée.
Ah,Je voulais dire l'hélice en rouge sur la photo afin de réaliser une hélicoïde sphérique si tu es d'accord...
Bonjour,
Une hélice ? où ça ? Un hélicoïde ? Lequel ? Défini comment?
Tu as été pêcher une perspective ici: ![]() et la courbe rouge est un chemin loxodromique sur une sphère qui n'a strictement rien à voir avec une hélice.
et la courbe rouge est un chemin loxodromique sur une sphère qui n'a strictement rien à voir avec une hélice.
Si tu veux voir des hélices sphériques, regarde ici: ![]()
Je te laisse imaginer un hélicoïde dont la directrice serait cette hélice...
Quant aux hélicoïdes, tu peux te documenter ici: ![]()
Tout ça pour te dire que quand on fait référence à des objets mathématiques précis (ici des courbes gauches, surfaces et autres), il faut savoir de quoi on parle.
De plus, on ne fait pas de la géométrie descriptive (je crois que c'est ton but ?) en bricolant sur un logiciel de CAO. Encore moins en dessinant des perspectives qui au mieux épatent le badaud et n'apportent rien à la la compréhension quantitative d'une pièce. On projette sur deux plans perpendiculaires (là je ne t'apprends rien) à l'aide par exemple d'un logiciel de géométrie comme GeoGebra (libre et gratuit et qu'on peut télécharger) ou au pire avec une feuille de papier et un crayon.
Au reste, si tu veux poser une nouvelle question qui ne concerne pas l'hélicoïde développable, ouvre un nouveau topic; celui ci est déjà bien assez long.
Bien entendu, je me réserve le droit d'y répondre ou pas... Il n'y a pas que moi sur le site.

Bonjour Lake et merci,
Oui tu as surement raison un logiciel tel que Geogebra serait sans doute plus adapté, mais en réalité rien ne vaut un tracé avec les instruments adéquats sur une bonne table à dessin et nous sommes tout à fait d'accord sur ce point... Enfin bon.Seulement je pense qu'il y a des erreurs d'interprétations concernant cette méridienne.Voici une imagetrouvé sur un de mes bouquin,après s'il faut créer un autre sujet et bien pourquoi pas.
Bonne réception et merci pour l'hélicoïde cylindre,je mettrais tout celà au propreau propre.
Bien cordialement.

Bon, tu m'obliges à manger mon chapeau 
J'ai en partie tort et tu as en partie raison: au vu des perspectives des hélices circulaires du site mathcurve de Robert Ferréol, je m'étais figuré un peu rapidement que ces hélices étaient infernales (avec points de rebroussement et autres fantaisies). Après ton extrait de bouquin, je suis allé y voir de plus près.
Avec GeoGebra, j'ai donc rentré les équations paramétriques (en et
en fonction des deux paramètres
et
(des curseurs pour GeoGebra) en sorte d'avoir une projection de ces hélices sur le plan
Le paramètre correspond au rayon de la sphère et n'intervient que pour un facteur d'échelle.
Par contre avec , j'ai eu une surprise:
Lorsque , par exemple, on obtient quelque chose de similaire aux images de mathcurve:
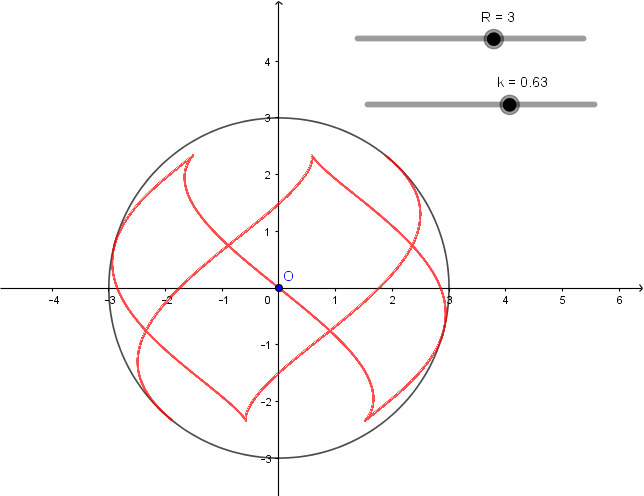
Par contre, lorsque , on obtient ceci:
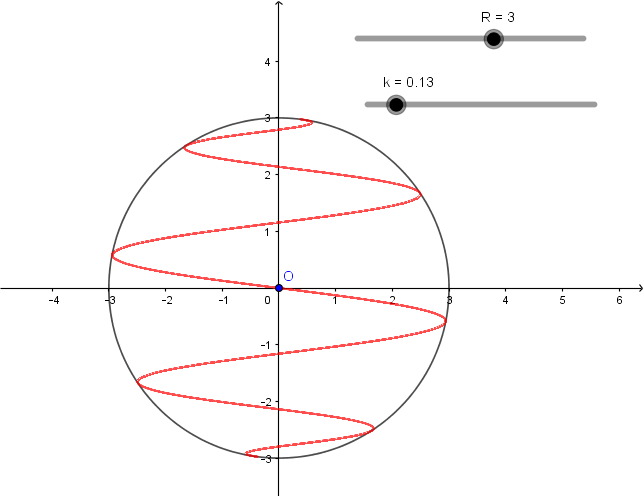
Et à mon grand dam, je suis bien obligé de reconnaître qu'on est en présence d'un hélice circulaire relativement "simple" et je te présente mes plus plates excuses.
Mais bon, ne te fait pas trop d'illusions: l'hélicoïde cylindrique (et en particulier l'hélicoïde développable) faisait intervenir des intersections droites/cylindres qui sont relativement "simples" à construire. De plus, la construction d'une l'hélice directrice à la surface d'un cylindre était aussi réalisable avec GeoGebra à peu de frais.
Avec une hélice sphérique, c'est une autre paire de manche; je vois déjà des intersections droites/sphère et des plans auxiliaires en pagaille qui vont me rendre la vie impossible d'autant plus que GeoGebra a aussi ses limites . A moins de rentrer directement les équations de cette hélice; mais là, c'est tricher: on ne fait plus de descriptive... Quant à la suite, ce sera pire...
En tout état de cause, j'espère t'avoir fait toucher du doigt les difficultés de mise en œuvre.
- Il faut commencer par choisir l'hélice sphérique directrice (en gros choisir le paramètre ).
- Décider comment sera engendré l'hélicoïde: des courbes? lesquelles? ou des droites? lesquelles? (s'appuyant sur l'axe de l'hélice, tangentes à l'hélice, autres?)
Bref, je ne la sens pas ton histoire...
Au reste, encore une fois, toutes mes excuses pour mon erreur; j'étais évidemment de bonne foi!
N'hésite pas à télécharger GeoGebra; l'apprentissage est très intuitif et la doc intégrée bien faite.
Une dernière chose sans grande importance: le mot "méridienne" intervient ici où la de manière anecdotique et n'a pas vraiment d'importance dans le sujet qui nous occupe.

j
e suis bien obligé de reconnaître qu'on est en présence d'un hélice sphérique relativement "simple"

Bonsoir Lake et encore merci pour tout.Oui je pense qu'ont se comprend et l'on préfère s'en tenir à la descriptive... Je pourrais peut être demander à mon ancien formateur de lIEF-CTF pour pourrait sans doute nous aider à bien démarrer réaliser cette épure d'hélicoïde sphérique ou bien chez mon fournisseur catalCAD....Mais, j'ai confiance en toi Lake pour ton esprit d'analyse et ta maitrise en matière de descriptive on peut s'en tirersi on veut vraiment.Bon,il ne faut pas que je brule les étapes alors, plutôt faire d'autres exercices un peu plus simples si j'ose dire cela.
Sincères Salutations.
Je crois que c'est raisonnable; ton hélicoïde sphérique me faisait quasiment peur 
Bonne continuation et à bientôt sur l':ilemaths; qui sait ? 
Je vois une surface réglée engendrée par une droite qui passe par le centre d'une sphère et qui s'appuie sur une courbe.
La courbe en question est-elle une hélice ? Comment a-t-elle été construite ?
Je n'en sais rien ... 
Bonjour pour créer cette hélicoïde j'ai lissé deux hélices de même pas, de deux hauteur différentes l'helice extérieur et bati sur le meme axe mais elle est plus longue et plus large que l'helice directrice ainsi sur cette vue en filaire on peut distinguer chaques courbe ainsi que leurvposition sur deux plans après je ne peut en dire plus sur la nomination de cette hélicoïde. ..
Bonjour david1972,
Juste un petit commentaire:
Tu nous parles d'hélicoïde engendré par une droite donc d'hélicoïde réglé.
Cette droite doit s'appuyer sur une hélice (la directrice) donc sur une courbe gauche dont les tangentes font un angle constant avec un plan fixe (c'est une des définitions d'une hélice).
Ici, on utilise une hélice sphérique c'est à dire une hélice tracée à la surface d'une sphère. Or une telle hélice a un pas qui n'est pas constant.
Or encore, tu nous dit:
j'ai lissé deux hélices de même pas
Si le pas de ta courbe (tracée sur une sphère) est constant, ce n'est pas une hélice.
En résumé, j'ai un gros doute sur la nature hélicoïdale de ta courbe directrice.
Et si mon doute est avéré, ta surface n'est pas un hélicoïde

Bon abandonnons cette géométrie, je posterai un nouveau sujet sur savoir comment tracé une épure d'une sphère géodésique.
Bonsoir Lake,bon l'idéal concernant cette « hélice sphérique ça serait que je te réalise une petite vidéo, mais je ne sais pas comment pourrai-je l'inséré en pièce jointe.Sinon j'ai envoyé un courriel afin de correspondre avec mon ancien formateur si ça te dit toi aussi.
Sinon l'hélice et de mêmes pas que la hauteursoit un tour complet que pour l'hélice directrice, peut-être pas trop visible sur les dernières capture d'écran. Quand je parle, de "lisser" cela signifie qu'en unissant deux courbes on obtient une surface réglée.
En divisant la hauteur de la sphère en nombres de partie égale,_8 par exemple, et en décrivant des cercles sur chaque diamètre on obtient des ponts de raccordement apparemment (j'ai vérifié sur l'image d'hier à 23H38 !


 géométrie en Bts
géométrie en Bts