Inscription / Connexion Nouveau Sujet
histoire sur les limites DM
On nomme quantité variable celle que l'on considère comme devant recevoir sucessivement plusieurs valeurs différentes les unes des autres.
On appelle au contraire quantité constante totue quantité qui reçoit une valeur fixe et déterminée.
Lorsque les valeurs succesivement attribuées à une même variable s'approchent indéfinniment d'une valeur fixe, de manière à finir par en différer aussi peu que l'on voudra, cette dernière est appelée la limite de toutes les autres.
Ainsi, la surface du cercle est la limite vers laquelle convergent les surfaces des polygones réguliers inscrits, tandis que le nombre de leurs côtés croît de plus en plus.
1)- interpréter ce qui est dit à propos de la surface du cercle considéré comme limite.
Pouriez vous m'aider svp
Bonjour,
il faut faire un dessin avec un cercle dans lequel tu traces différents polynômes réguliers (le cercle est le cercle circonscrit à tous ces polynômes) :
- triangle isocèle (3 côtés),
- carré (4 côtés),
- pentagone régulier (5 côtés),
- hexagone régulier (6 côtés),
- etc ....
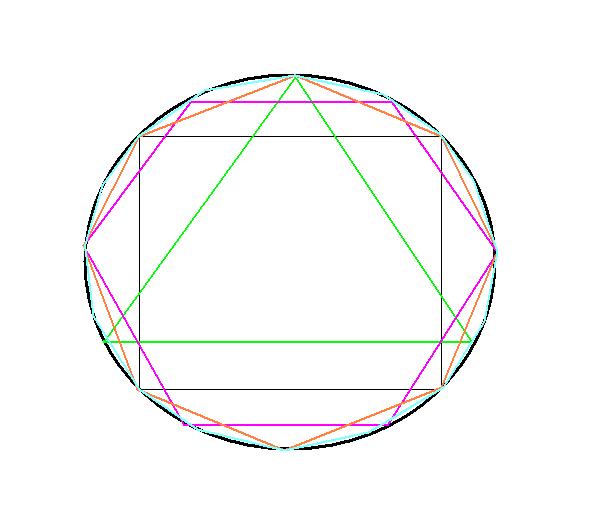
j'ai essayé de faire un dessin vite fait ... j'y ai mis un triangle isocèle, un carré, un hexagone, un octogone et un hexadécagone (si je ne me trompe pas) (un polygône à 16 côtés)
Sauf erreur,
ManueReva