Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques DétentePour discuter des JFF, des problèmes intéressants. ExercicesExercices ludiques [tout]Lister tous les topics de mathématiques
Niveau exercices
Partager :

inégalité sympa

Posté par
jarod128 27-07-20 à 17:29

Bonjour, je vous propose de démontrer l'inégalité suivante. J'ai une solution mais je voulais voir si vous m'en proposez d'autres. Donc n'oubliez pas de blanker.
Montrer que pour a réel et b réel strictement positif, on a:

|(1+b)^{ia}-1| \leq |a|b

Posté par
Alexiquere : inégalité sympa 27-07-20 à 21:16

Bonsoir,

on pose x=a\ln(1+b). Alors
|(1+b)^{ia}-1| = |e^{ix}-1| = |e^{\frac{ix}{2}}(e^{\frac{ix}{2}}-e^{-\frac{ix}{2}}| = 2|\sin(\frac{x}{2})| \geq |x| =|a|\ln(1+b)\geq |a|b grâce à |\sin(u)|\geq |u| et \ln(1+u)\geq u

Posté par
Alexiquere : inégalité sympa 27-07-20 à 21:18

Désolé, j'ai fait "poster" au lieu de "aperçu". Changer les sens.

on pose x=a\ln(1+b). Alors
|(1+b)^{ia}-1| = |e^{ix}-1| = |e^{\frac{ix}{2}}(e^{\frac{ix}{2}}-e^{-\frac{ix}{2}})| = 2|\sin(\frac{x}{2})| \leq |x| =|a|\ln(1+b)\leq |a|b grâce à |\sin(u)|\leq |u| et \ln(1+u)\leq u

Posté par
jarod128re : inégalité sympa 27-07-20 à 22:33

Jolie. C'est ce que j'ai trouvé. J'ai mis pas mal de temps. Je me demandais s'il y avait un autre moyen sans l'inégalité avec le sinus

Posté par
LittleFoxre : inégalité sympa 28-07-20 à 15:14


On peut réécrire (1+b)^{ia} = e^{ia\ln(1+b)}.
C'est à dire qu'on parcourt sur un cercle unitaire une distance de a\ln(1+b) en partant du point complexe 1.

La distance le long d'une courbe est plus grande que le long du segment qui relie l'origine. Et donc |(1+b)^{ia} - 1| \le |a\ln(1+b)|

Puisque b est positif, on a |a\ln(1+b)| = |a|\ln(1+b) \le |a|b.

On a donc l'inégalité |(1+b)^{ia} - 1| \le |a|b.

C'est visuel et sans sinus

Posté par
jarod128re : inégalité sympa 28-07-20 à 15:37

Bonjour Littlefox, c'est ce type de démo que je cherchais mais peux tu developper: La distance le long d'une courbe est plus grande que le long du segment qui relie l'origine.  Je ne vois pas le segment en question. Merci

Posté par
LittleFoxre : inégalité sympa 28-07-20 à 15:56


Si on part du point A en suivant la courbe jusqu'à un point B. La distance le long de la courbe sera toujours plus grande que la distance le long du segment entre A et B (autrement dit la distance la plus courte est la ligne droite).

Je n'aurai pas du utiliser le mot "origine" pour le point de départ A.

Ici A est le point complexe 1 et B le point sur le cercle unitaire (1+b)^{ia}.

Posté par
jarod128re : inégalité sympa 28-07-20 à 16:00

Ok, c'était le mot origine qui m'embêtait.
Merci.

Posté par
Alexiquere : inégalité sympa 28-07-20 à 18:16

@LittleeFox : ce que tu dis, c'est exactement la démonstration géométrique de \sin(\theta)\leq \theta (arc de cercle d'angle \theta plus grand que le segment "directe" de longueur \sin(\theta) donc c'est pas vraiment une preuve différente.

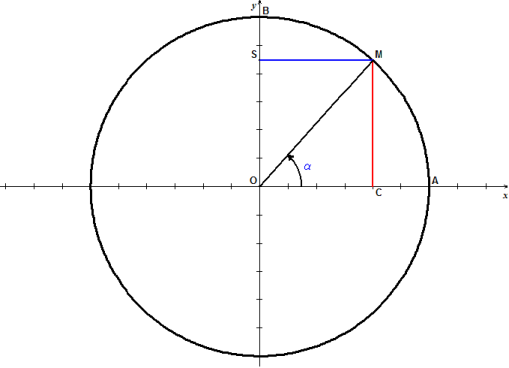
Ci-dessous, \alpha = \text{arc}(MA) \geq MA \geq MC = \sin(\alpha) car l'hypothénuse MA est plus grande que le côté MC.

inégalité sympa

Posté par
Prototipe19re : inégalité sympa 28-07-20 à 23:24

LittleFox @ 28-07-2020 à 15:56


Si on part du point A en suivant la courbe jusqu'à un point B. La distance le long de la courbe sera toujours plus grande que la distance le long du segment entre A et B (autrement dit la distance la plus courte est la ligne droite).

Je n'aurai pas du utiliser le mot "origine" pour le point de départ A.

Ici A est le point complexe 1 et B le point sur le cercle unitaire (1+b)^{ia}.


Bonjour jaimerai savoir la mesure du segment est  (1+b)^{ia}-1 ?

Posté par
Prototipe19re : inégalité sympa 28-07-20 à 23:24

Du segment [AB]

Posté par
LittleFoxre : inégalité sympa 29-07-20 à 11:51

Presque :

|AB| = |(1-b)^{ia} -1|

Posté par
Prototipe19re : inégalité sympa 29-07-20 à 12:18

LittleFox

LittleFox @ 29-07-2020 à 11:51

Presque :

|AB| = |(1-b)^{ia} -1|


Super et par mes propriété d'analyse complex votre démo est élégante


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !