Niveau Reprise d'études

interpolation

Posté par machintruc 27-12-18 à 11:06

Bonjour

il n'y a évidemment pas de solution unique au problème ci-dessous
je trouve la solution que je propose ici bien compliquée
ceci dit si vous en avez une plus simple je vous remercie d'avance
certes ma solution fonctionne bien et je peux la placer sur géogebra
mais ça serait mieux si on pourrait trouver quelque chose de plus simple

énoncé

On se donne un intervalle fermé et borné $I$ de $\mathbb {R}$
on notera
$i_1$ (resp. $i_2$ ) est la borne inférieure (resp. supérieure) de $I$

On se donne un élément quelconque $\left(k_1k_2pq\right)$ de $\mathbb {R}^4$

Construire une application $f:\mathbb {R}\rightarrow \mathbb {R}$ dérivable sur $\mathbb {R}$
qui vérifie
$f\left(i_1\right)=k_1$
$f\left(i_2\right)=k_2$
$f^{\prime}\left(i_1\right)=p$
$f^{\prime}\left(i_2\right)=q$

et déterminer un intervalle fermé et borné $J$ de $\mathbb {R}$
qui contient l'ensemble d'appplication de $f$

un exemple calculé sous geogebra

Je propose donc ici une solution à cet énoncé
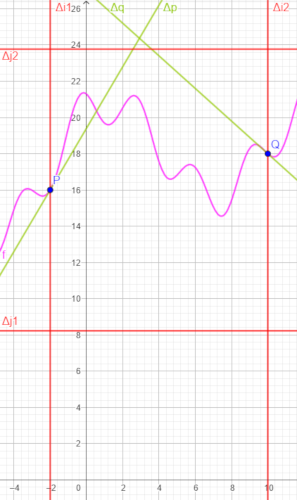
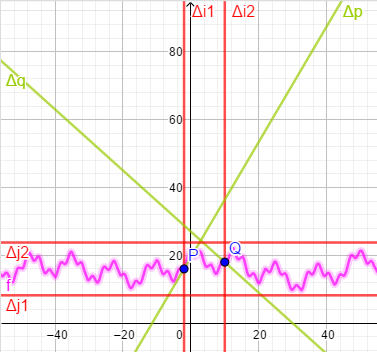
Dans l'image ci-dessous les droites $\Delta j_1$ et $\Delta j_2$
dépendent des paramètres donnés dans l'énoncé (elles ne sont pas calculées au hasard)
mais pas seulement :
elles dépendent aussi d'un nombre réel strictement positif
(c'est pour cela que mon calcul me donne autant d'intervalles $J$ possibles qu'il y a de réels strictement positifs
i.e. une infinité non dénombrable)
de la même manière à partir d'une infinité dénombrable particulière de couples de relatifs et pour les paramètres donnés dans l'énoncé j'ai une infinité dénombrable de fonctions possibles

interpolation

proposition de solution

On se donne $\left(un)\right)\in \mathbb {Z}^2$ tel que

$u\in \{0,1,-1\}$
lorsque $u=0$ alors $n\in \mathbb {Z}^*$ sinon $n\in \mathbb {N}$

et on se donne un réel strictement positif $\epsilon >0$

alors

On pose les seize réels suivant $a,b,c,v,w,t,\alpha , \beta$
$t_i$ avec $i$ de 1 à 8

de la façon suivante

$a=i_2-i_1$
$b=k_2-k_1$
$c=q-p$

Lorsque $u=0$ alors on pose $v=\dfrac {n+\sqrt {n^2+\pi}}{2}$ sinon $v=\dfrac {2+n+u.\sqrt {\left(2+n\right)^2-\pi}}{2}$

$w=\dfrac {\pi}{4v}$
$t=w.sin(2\pi w)-v.sin(2\pi v)$

(une petite remarque qui se démontre on vérifiera toujours $t\neq 0$ )
(ceci dit il y a d'autres choses à dire mais là je ne fais que proposer une solution au problème)

$t_1=\dfrac {2+7t}{4t}.k_1-\dfrac {2+3t}{4t}.k_2+\dfrac {2-t}{2\pi t}.a.p-\dfrac {1}{\pi t}.a.q$
$t_2=\dfrac {7t-2}{4t}.k_1+\dfrac {2-3t}{4t}.k_2-\dfrac {2+t}{2\pi t}.a.p+\dfrac {1}{\pi t}.a.q$
$t_3=\dfrac {2+9t}{4t}.k_1-\dfrac {2+5t}{4t}.k_2+\dfrac {2+t}{2\pi t}.a.p-\dfrac {1}{\pi t}.a.q$
$t_4=\dfrac {9t-2}{4t}.k_1+\dfrac {2-5t}{4t}.k_2+\dfrac {t-2}{2\pi t}.a.p+\dfrac {1}{\pi t}.a.q$
$t_5=\dfrac {2-t}{4t}.k_1+\dfrac {5t-2}{4t}.k_2+\dfrac {2-t}{2\pi t}.a.p-\dfrac {1}{\pi t}.a.q$
$t_6=-\dfrac {2+t}{4t}.k_1+\dfrac {2+5t}{4t}.k_2-\dfrac {2+t}{2\pi t}.a.p+\dfrac {1}{\pi t}.a.q$
$t_7=\dfrac {2+7t}{4t}.k_1+\dfrac {3t-2}{4t}.k_2+\dfrac {2+t}{2\pi t}.a.p-\dfrac {1}{\pi t}.a.q$
$t_8=\dfrac {t-2}{4t}.k_1+\dfrac {3t+2}{4t}.k_2+\dfrac {t-2}{2\pi t}.a.p+\dfrac {1}{\pi t}.a.q$

$\alpha =max(t_1,t_2,t_3,t_4,t_5,t_6,t_7,t_8)$
$\beta =min(t_1,t_2,t_3,t_4,t_5,t_6,t_7,t_8)$

on pose les deux applications dérivables suivantes $h:\mathbb {R}\rightarrow \mathbb {R}$ et $g:\mathbb {R}\rightarrow \mathbb {R}$
avec leurs dérivées respectives $h^{\prime}$ et $g^{\prime}$

$h(x)=k_1+b.sin\left(\dfrac {\pi (x-i_1)}{2a}  \right)+\left(\dfrac {pa}{2\pi}- \dfrac {b}{4} \right).sin\left( \dfrac {2\pi(x-i_1}{a}\right)$
$+\dfrac {1}{t}.\left( \dfrac {b}{4}+ \dfrac {ac}{2\pi}\right).\left( cos\left( \dfrac {2\pi v(x-i_1)}{a} \right)-cos\left( \dfrac {2\pi w(x-i_1)}{a} \right) \right)$

$h^{\prime}(x)=\dfrac {\pi b}{2a}.cos\left(\dfrac {\pi (x-i_1)}{2a}  \right)+\left(p-\dfrac {\pi b}{2a}\right).cos\left( \dfrac {2\pi(x-i_1}{a}\right)$
$+\dfrac {1}{t}.\left( \dfrac {\pi b}{2a}+c\right).\left(w.sin\left( \dfrac {2\pi w(x-i_1)}{a} \right)-v.sin\left( \dfrac {2\pi v(x-i_1)}{a} \right) \right)$

1.Lorsque $\epsilon = 1$ on pose $j_1=\beta$ et $j_2=\alpha$
dans ce cas là on n'utilise pas la fonction $g$

sinon on pose $\theta =\dfrac {\pi k}{a}$ avec $k \in \mathbb {N}^*$ pair (attention k est pair)

2.Lorsque $\epsilon < 1$ on pose $\varphi \in \{-\theta.i_1,-\theta.i_2\}$
$j_1=\beta$
$j_2=\alpha$

alors
$g(x)=\dfrac {1-\epsilon}{2}.cos \left(\theta .x+\varphi \right)+\dfrac {\epsilon +1}{2}$
$g^{\prime}(x)=\dfrac {\epsilon -1}{2}.\theta .sin \left( \theta .x+\varphi \right)$

3.Lorsque $\epsilon > 1$ on pose $\varphi \in \{\pi-\theta.i_1,\pi-\theta.i_2\}$
$j_1=\dfrac {\beta - \alpha}{2}.\epsilon +\dfrac {\alpha + \beta}{2}$
$j_2=\dfrac {\alpha -\beta}{2}.\epsilon +\dfrac {\alpha + \beta}{2}$

alors
$g(x)=\dfrac {\epsilon -1}{2}.cos \left(\theta .x+\varphi \right)+\dfrac {\epsilon +1}{2}$
$g^{\prime}(x)=\dfrac {1-\epsilon }{2}.\theta .sin \left( \theta .x+\varphi \right)$

L'application que l'on recherche est donnée par l'expression

Lorsque $\epsilon = 1$ alors $f(x)=h(x)$ et   $f^{\prime}(x)=h^{\prime}(x)$

sinon

$f(x)=g(x).\left(h(x)-\dfrac {\alpha+\beta}{2} \right)+\dfrac {\alpha+\beta}{2}$
$f^{\prime}(x)=g^{\prime}(x).\left(h(x)-\dfrac {\alpha+\beta}{2} \right)+g(x).h^{\prime}(x)$

enfin ce qui concerne la deuxième question

$J$ est un intervalle fermé et borné contenant l'ensemble d'application de $f$
$j_1$ (resp. $j_2$ ) est la borne inférieure (resp. supérieure) de $J$

Posté par re : interpolation 27-12-18 à 12:07

petite précision là dans mon bidule je peux construire une infinité dénombrable de fonctions h (c'est ce que je voulais dire dans mon exemple )

mais une infinité non dénombrable de fonctions f (puisque f dépend aussi du réel strictement positif $\epsilon$ que je peux choisir comme je veux sans que ce que demande l'énoncé gêne en quoi que ce soit )

bon sinon après ça m'étonnerait beaucoup qu'il n'y ait pas des solutions plus simples

Posté par re : interpolation 27-12-18 à 12:27

Une heuristique qui marche pas mal dans ce genre de problème est de raisonner en terme de dimension.
La dimension des fonctions dérivables sur R est infinie non dénombrable (prendre par exemple (x ->exp(tx), t réel) qui est clairment libre) du coup y a fort a parier que T:f->(f(a), f(b), f'(a), f'(b)) (je change un peu les notations) soit surjective vu que l'espace d'arrivée est de dimension 4. Dans tous les cas cela t'assure que la dimension de noyau est infinie non dénombrable donc si tu trouves une solution tu en as une infinité non dénombrable.

Une idée par trop bète consiste a regarder ce qu'il se passe sur les polynomes de degré au plus 3 vu que c'est un espace de dimension 4.
Evidement il est interessant de prendre une base adapté à la situation.
Comme (X-b), (X-a), (X-a)^2(X-b), (X-b)^2(X-a).
Pourquoi cette base, parce que l'application T se calcule facilement dans cette base (j'ecris les vecteur en ligne) en effet on T(X-b)=((a-b), 0, 1, 1) T(X-a)=(0, b-a, 1, 1 )
T((X-a)^2(X-b))=(0,0,0, (b-a)^2) et T((X-a)(X-b)^2)=(0,0, (b-a)^2, 0).
On voit facilement que l'image de T est donc de rang 4 (ce qui prouve au passage que la famille qu'on avait considéré est bien une base de l'espace des polynome de degré au plus 3). Et donc que T est surjective. Donc tu sais qu'il existe des polynome de degré 3 qui répondent à la question et qu'ils sont uniques.
Pour les trouver tu n'a qu'a résoudre un système (ou etre un peu malin).

Posté par re : interpolation 27-12-18 à 12:42

Merci Poncargues

Ta solution me plait énormément : une manière d'appliquer l'algèbre à ce problème

... au lieu de s'en tenir bêtement à la trigo et au final ça va simplifier énormément une solution possible à ce problème

Posté par re : interpolation 29-12-18 à 07:09

juste pour compléter un peu ma solution (sans trop l'exploiter vu que Poncargues me propose quelque chose de plus élégant comme solution )

à un moment donné on tombe sur

$\alpha =max(t_1,t_2,t_3,t_4,t_5,t_6,t_7,t_8)$
$\beta =min(t_1,t_2,t_3,t_4,t_5,t_6,t_7,t_8)$

on peut demander à sa machine de calculer ça mais sinon on peut aussi exprimer une formule donnant $\alpha$ et   $\beta$
en fait c'est ce que j'ai fait sur geogebra

la formule en question utilise les quatres opérations de base +-x/ et la fonction partie entière inférieure
je propose donc cette formule pour le cas de ma solution

Attention cette formule ne fonctionne pas dans un autre contexte car les treize réels   $c_i$   ci-dessous
dépendent du contexte de ce problème et ne pourra pas servir pour déterminer des max et des min
Par ailleurs on remarquera ici que calculer un max permet de trouver sans calcul le min (et inversement)
car il y a une symétrie dans les $t_i$

alors on pose les treize réels   $c_i$
$c_1=-\pi b-2ac$
$c_2=\pi tb-2tap$
$c_3=-2\pi b+\pi tb-4ac-2tap$
$c_4=-\pi tb$
$c_5=-\pi b-2\pi tb-2ac$
$c_6=-3\pi tb-2tap$
$c_7=-2\pi b-3\pi tb-4ac-2tap$
$c_8=2\pi b +\pi tb+4ac-2tap$
$c_9=\pi b-2\pi tb+2ac$
$c_{10}=2\pi b-3\pi tb+4ac-2tap$
$c_{11}=-5\pi tb+2tap$
$c_{12}=-2\pi b-5\pi tb-4ac+2tap$
$c_{13}=2\pi b-5\pi tb+4ac+2tap$

puis on pose les vingt six entiers naturels $a_i \in \{0,1\}$ et $b_i \in \{0,1\}$

$a_i=\left\lfloor\dfrac{2\left\lfloor\dfrac{c_i+\left|c_i \right|+1}{\left|c_i \right|+1}\right\rfloor}{\left\lfloor\dfrac{c_i+\left|c_i \right|+1}{\left|c_i \right|+1}\right\rfloor +1}\right\rfloor$
$b_i=\left\lfloor\dfrac{2\left\lfloor\dfrac{\left|c_i \right|+1}{c_i+\left|c_i \right|+1}\right\rfloor}{\left\lfloor\dfrac{\left|c_i \right|+1}{c_i+\left|c_i \right|+1}\right\rfloor +1}\right\rfloor$

Alors

$\alpha =b_1b_2b_3b_4b_5b_6b_7t_1+a_1b_2b_4b_6b_8b_9b_{10}t_2$
$+b_1a_2b_4b_5a_8b_{11}b_{12}t_3+a_1a_2a_3b_4b_9b_{11}b_{13}t_4$
$+b_1b_2b_3a_4a_9a_{11}a_{13}t_5+a_1b_2a_4a_5b_8a_{11}a_{12}t_6$
$+b_1a_2a_4a_6a_8a_9a_{10}t_7+a_1a_2a_3a_4a_5a_6a_7t_8$

$\beta =a_1a_2a_3a_4a_5a_6a_7t_1+b_1a_2a_4a_6a_8a_9a_{10}t_2$
$+a_1b_2a_4a_5b_8a_{11}a_{12}t_3+b_1b_2b_3a_4a_9a_{11}a_{13}t_4$
$+a_1a_2a_3b_4b_9b_{11}b_{13}t_5+b_1a_2b_4b_5a_8b_{11}b_{12}t_6$
$+a_1b_2b_4b_6b_8b_9b_{10}t_7+b_1b_2b_3b_4b_5b_6b_7t_8$

Posté par re : interpolation 29-12-18 à 08:38

...ensuite
on était tombé sur deux entiers relatifs $u$ et $n$ qui permettaient de calculer un réel $v$
là encore on peut simplifier car l'embêtant c'était que $v$ était donné par deux formules différentes selon que $u$ soit nul ou pas et de plus il fallait bien faire attention à la valeur de $n$ qui dans le cas $u=0$ alors il fallait que $n$ ne soit pas nul et dans le cas $u\neq 0$ il fallait que $n$ soit un entier naturel

bref tout un bordel si on place ça dans sa machine

une astuce consiste ici à se débarrasser définitivement de $u$ et $n$ et en se donnant un complexe et une application qui permette d'avoir comme image de ce complexe par cette application une valeur $v$ qui soit toujours valable et qui permette de parcourir toutes les valeurs $v$ possibles

l'astuce ici consiste à utiliser la solution donné à l'énoncé que j'ai placé sur un autre sujet (certes ma solution est une formule un peu longue mais la machine calculera ça sans aucun problème et tout ça sans avoir à utiliser des trucs du genre IF THEN et autres conditionnelles qui donne du boulot à écrire dans la programmation et qui en plus allonge le temps de calcul et pour peu qu'on utilise plusieurs calculs de cette fonction va devenir coûteux en variables

l'énoncé et la solution (elle n'est pas unique) est donnée dans l'un des sujets ouvert cette nuit (donc facile à trouver pour ceux que ça intéresse)

Posté par re : interpolation 31-12-18 à 10:56

Bonjour

je ne voulais rien dire  car cela ne changeait rien au résultat demandé mais je ne pouvais laisser cette erreur

je m'explique :

j'avais donné un autre moyen de calculer $\alpha$ et $\beta$

on peut utiliser ce calcul là pour ce qui est demandé dans l'énoncé et donc la solution de ce problème avec ce calcul là sera correct (c'est dans ce sens là que j'ai dit que cela ne change rien)

par contre il est faux d'affirmer que les valeurs $\alpha$ et $\beta$ ainsi exprimées avec ce calcul là donneront toujours

$\alpha =max \left(t_1,t_2,t_3,t_4,t_5,t_6,t_7,t_8 \right)$
$\beta =min \left(t_1,t_2,t_3,t_4,t_5,t_6,t_7,t_8 \right)$

mais bon ce n'est pas grave car on se fiche ici que par exemple on obtienne

$\alpha = n.max \left(t_1,t_2,t_3,t_4,t_5,t_6,t_7,t_8 \right)$
$\beta  = n.min \left(t_1,t_2,t_3,t_4,t_5,t_6,t_7,t_8 \right)$

où n est un entier naturel non nul

et c'est justement ce qui peut arriver dans certains cas avec mon calcul

Posté par re : interpolation 31-12-18 à 23:14

Bonjour

cependant en modifiant un peu

en posant

$A^{\prime}=b_1b_2b_3b_4b_5b_6b_7t_1+a_1b_2b_4b_6b_8b_9b_{10}t_2$
$+b_1a_2b_4b_5a_8b_{11}b_{12}t_3+a_1a_2a_3b_4b_9b_{11}b_{13}t_4$
$+b_1b_2b_3a_4a_9a_{11}a_{13}t_5+a_1b_2a_4a_5b_8a_{11}a_{12}t_6$
$+b_1a_2a_4a_6a_8a_9a_{10}t_7+a_1a_2a_3a_4a_5a_6a_7t_8$

$A=b_1b_2b_3b_4b_5b_6b_7+a_1b_2b_4b_6b_8b_9b_{10}$
$+b_1a_2b_4b_5a_8b_{11}b_{12}+a_1a_2a_3b_4b_9b_{11}b_{13}$
$+b_1b_2b_3a_4a_9a_{11}a_{13}+a_1b_2a_4a_5b_8a_{11}a_{12}$
$+b_1a_2a_4a_6a_8a_9a_{10}+a_1a_2a_3a_4a_5a_6a_7$

$B^{\prime}=a_1a_2a_3a_4a_5a_6a_7t_1+b_1a_2a_4a_6a_8a_9a_{10}t_2$
$+a_1b_2a_4a_5b_8a_{11}a_{12}t_3+b_1b_2b_3a_4a_9a_{11}a_{13}t_4$
$+a_1a_2a_3b_4b_9b_{11}b_{13}t_5+b_1a_2b_4b_5a_8b_{11}b_{12}t_6$
$+a_1b_2b_4b_6b_8b_9b_{10}t_7+b_1b_2b_3b_4b_5b_6b_7t_8$

$B=a_1a_2a_3a_4a_5a_6a_7+b_1a_2a_4a_6a_8a_9a_{10}$
$+a_1b_2a_4a_5b_8a_{11}a_{12}+b_1b_2b_3a_4a_9a_{11}a_{13}$
$+a_1a_2a_3b_4b_9b_{11}b_{13}+b_1a_2b_4b_5a_8b_{11}b_{12}$
$+a_1b_2b_4b_6b_8b_9b_{10}+b_1b_2b_3b_4b_5b_6b_7$

et là on a bien les deux égalités

$\alpha=\dfrac {A^{\prime}}{A}=max \left(t_1,t_2,t_3,t_4,t_5,t_6,t_7,t_8 \right)$

$\beta =\dfrac {B^{\prime}}{B}=min \left(t_1,t_2,t_3,t_4,t_5,t_6,t_7,t_8 \right)$

ici on a toujours $A\in \mathbb {N}^*$ et $B\in \mathbb {N}^*$