Strictement parlant, la transposée agit sur le dual de E, pas sur E.
Si f est une application linéaire de E dans F, la transposée de f est une application linéaire de F* dans E* qui envoie sur . C'est un concept proche mais différent de celui d'adjoint d'un opérateur dans un espace de Hilbert, qui lui, est défini par son action en fonction du produit scalaire <Ax,y> = <x,A*y>, et c'est encore autre chose si tu généralises cela aux C*-algèbres...

Heureusement, en dimension finie, on peut toujours identifier E à E*. Et pour les espaces de Hilbert usuels, ils sont réflexifs, séparables, etc. Tout ce qu'il faut pour que H coincide avec son dual topologique. Donc moralement, on peut voir ladjonction/la trasposition comme des opérations sur H et E respectivement.


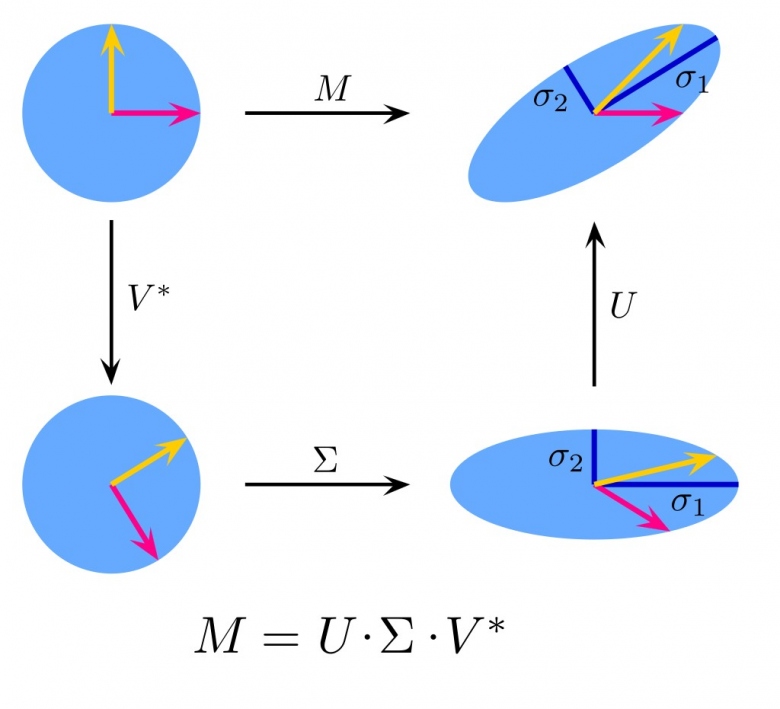
Maintenant pour le sens géométrique, regarde l'image image Wikipedia jointe. Le but de la transformation M est de faire un chagement de base pour dilater le disque unité dans deux directions pas forcément orthogonales. On procède en trois étapes : d'abord on fait tourner le disque d'un quart de tour dans le sens horaire. Ensuite on l'étire vers la droite et on l'écrase verticalement. Et enfin on tourne, cette fois dans le sens direct, de pi/4.


Si on avait fait ces étapes à l'envers, on aurait eu aussi un ovale, mais qui pointerait vers le bas.
Si on veut obtenir le même résultat, il faut remplacer l'action de par celle d'une autre matrice, , qui consiste à écraser le cercle horizontalement et à l'étirer verticalement. Un retournement qui se voit dans la formule , qui veut dire que pour faire AB à l'envers, je ne fais pas BA, mais XY avec X un truc qui remplace B et Y un truc qui remplace A.


Pour les adjoints c'est pareil. Pour savoir ce que fait A globalement, on regarde ce qu'il fait à x du point de vue du vecteur y, c'est à dire le projeté <Ax,y>. L'opération adjointe de A, ça consiste à regarder à quoi ressemble x du point de vue du vecteur A*y.
A   : je transforme et je regarde le résultat, dans un base fixe
A* : je regarde le vecteur que A transforme, dans une base transformée

Bonsoir,

Une réponse partielle :
Si est un endomorphisme linéaire, sa transposée est l'endomorphisme de l'espace dual défini par pour toute forme linéaire sur .
Si est un espace euclidien (de dimension finie), le produit scalaire fournit une identification canonique de avec (le vecteur identifié à la forme linéaire ), ce qui permet de voir comme l'endomorphisme de défini par .
Bon, je pense que tu vas rester sur ta faim. Tant pis !

Bonsoir , merci pour vos réponses . Je sais que E , E* et { x-> (a|x) , a dans E } sont isomorphes et j'accepte  tout à fait ces résultats  .
Je ne comprend pas cependant pourquoi il y a un passage par les formes linéaires , je ne vois pas   le lien entre  le " changement de base " et autres transformation de l'espace évoqué par ulmière et le fait d'envoyer une forme linéaire phi sur phi o f.