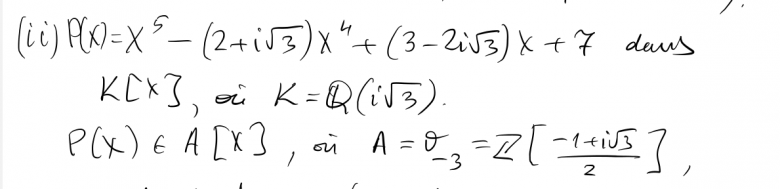
Bonjour Nilav,

Je ne suis pas sûr mais je dirais que



Ici, tu as



Pour montrer que P(X) est dans A[X] il faut montrer que les coefficients de P sont dans A. Par exemple car si je prends alors . Je te laisse chercher Q pour montrer que les autres coefficients de P(X) sont dans A.

Indication : il suffit de considérer Q(X) de degré au plus 1, vois par exemple ce que donne Q(X)=a + 2bX.

Il faut remplacer les par .

Merci! Je comprend la méthode mais d'où sort cet anneau? La question n'avait pas d'indication donc je ne comprend pas trop le cheminement !

La question c'est quoi précisément ?

A priori, sans avoir le contexte, on peut se demander pourquoi n'avoir pas choisi (anneau non principal) ?

La question exacte était "X^5 - blabla + 7 est il irréductible dans Q(i√3) "

D'accord. Ici l'intérêt de l'anneau A, c'est qu'il est factoriel (c'est l'anneau des entiers d'Eisenstein). En particulier on peut utiliser appliquer le critère d'Eisenstein pour monter que est irréductible (s'il l'est) sur K (corps des fractions de A).

Sur un anneau non factoriel, le critère d'Eisenstein est a priori faux.

Ok merci beaucoup ! C'est encore un peu obscur pour moi de penser à introduire ce genre d'anneau mais j'imagine que ça viendra 😁

Bonsoir,

est l'anneau des entiers du corps de nombres   : c'est le sous-anneau de ce corps formé des éléments qui sont racines d'un polynôme unitaire à coefficients entiers. Vois-tu quel polynôme à coefficients entiers dans le cas de ?

?

Exact.

Cet anneau des entiers contient strictement .
Un joli dessin : dessiner les deux anneaux dans (un point pour chaque élément de l'anneau). On obtient deux réseaux, l'un avec une maille deux fois plus grande que celle de l'autre.

Ça dépasse pour l'instant mon niveau de compétence
Je me suis arrêté à la réalisation des corps finis.