Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Licence Maths 1e ann ProbabilitésTopics traitant de probabilités [tout]Lister tous les topics de mathématiques
Niveau Licence Maths 1e ann
Partager :

Jeu de probabilités

Posté par
Ennydra 17-02-17 à 17:29

Bonjour.

Je suis confrontée à un exercice très complexe en probabilités, je ne vois pas comment commencer pour traiter cet exercice...

On considère le jeu suivant. On donne au premier joueur un nombre X_1 ~ Unif[0,1]. Le joueur découvre ce nombre, il peut choisir de le garder, auquel cas son score final sera ce nombre X_1, ou bien il peut choisir de retenter sa chance, auquel cas il se verra attribuer un nombre Y_1 ~ Unif[0,1], indépendant de X_1.

Similairement, le deuxième joueur reçoit X_2 ~ Unif[0,1] indépendante de (X_1, Y_1) qu'il peut choisir de garder, sinon il se verra attribuer Y_2 ~ Unif[0,1], indépendante de (X_1, Y_1, X_2).

On précise qu'au moment où il joue, un joueur ne connaît pas les tirages de son adversaire, il ne pourra que comparer son score final à celui de son adversaire. Le gagnant est évidemment le joueur qui obtient le score le plus grand.

Une stratégie naturelle consiste à garder le premier tirage si et seulement si il dépasse un seuil \alpha \in (0,1). On note S_{\alpha} le score obtenu en suivant cette stratégie.

1. Montrer que la variable S_{\alpha} possède une densité f_{\alpha} que l'on explicitera.

2. Exprimer la probabilité de gain pour le premier joueur lorsqu'il adopte la stratégie de seuil \alpha, et lorsque le deuxième joueur adopte la stratégie de seuil 0. En déduire un \alpha optimal lorsque le deuxième joueur rejette systématiquement le premier tirage.

3. On suppose que le joueur 1 adopte la stratégie de seuil \alpha, tandis que le joueur 2 adopte la stratégie de seuil \beta \leq \alpha.

Montrer que la probabilité p_1 que le joueur 1 l'emporte est :
p_1 = \int_0^1 f_{\alpha}(x) ( \int_0^x f_{\beta}(y)dy) dx.

En déduire que :
p_1 = \dfrac{1}{2} + \dfrac{\alpha + \beta}{2}(1-\alpha-\alpha \beta).

On note \alpha_2 = \dfrac{\sqrt{5}-1}{2}. Expliquer pourquoi la stratégie de seuil \alpha_2 est optimale.

Merci d'avance pour toute indication...

Posté par
lionel52re : Jeu de probabilités 17-02-17 à 17:40

Hello

Je te conseille de raisonner par fonction de répartition. Soit x dans [0,1]

\mathbb{P}(S_a \leq x) = \mathbb{P}(X_1 \leq x \cap X_1 > a)  +  \mathbb{P}(X_2 \leq x \cap X_1 \leq a)

Le second terme est facile à calculer par indépendance de X1 et X2
Le premier terme bah ça dépend si x est plus petit ou grand que a

Posté par
verdurinre : Jeu de probabilités 18-02-17 à 21:40

Bonsoir.

Attention, il y a une faute de frappe :

p_1 = \dfrac{1}{2} + \dfrac{\alpha{\color{red} -} \beta}{2}(1-\alpha-\alpha \beta)

Posté par
grenadine75re : Jeu de probabilités 18-02-17 à 22:00

Bonsoir,

je suis en licence également et je fais le même exercice, lorsque j'ai voulu faire P(xS) je trouve X1(1-) + X2  alors que d'après la question3. je suis censé trouver  \frac{1}{2}+ \frac{\alpha }{2}(1-\alpha ), est-ce quelqu'un peut me dire pourquoi P(xX1) ne dépend pas de X1.

(Pour mes calculs j'ai fait f=1 )

Merci d'avance,

Posté par
verdurinre : Jeu de probabilités 18-02-17 à 22:31

Bonsoir,

la question 3 ne donne pas la fonction de répartition de S, mais la probabilité de gain pour le joueur ayant le seuil le plus grand.

Pour déterminer la fonction de répartition de S et donc sa densité, le plus simple me semble d'utiliser la méthode indiquée par lionel52.

Une indication

\mathbb{P}(X_1 \leq x \cap X_1 > a)=\mathbb{P}(a<X_1\le x)=\begin{cases}0 &\text{si } x\le a\\ \cdots &\text{si } a\le x\le1\end{cases}

Posté par
grenadine75re : Jeu de probabilités 18-02-17 à 23:15

Bonsoir,

d'accord je ne dois pas bien comprendre les termes je pensais que la fonction de répartition c'était F(x)=f dx
et que  f la focntion densité suit une loi uniforme sur [0,1] donc f=1 que x=X1 ou X2

Du coup j'ai un doute sur ce que veut dire  P(Sx) mais j'aurait dit 1- sur [,1]

et du coup P(X2xX1)= ?

Posté par
verdurinre : Jeu de probabilités 19-02-17 à 10:26

Par définition la fonction de répartition FX d'une variable aléatoire réelle  X est définie sur R par :
quelque soit t réel FX(t)=P(Xt)

Si FX est dérivable presque partout alors X a une densité f qui est la dérivée de la fonction de répartition.
On a alors F_X(t)=\int_{-\infty}^t f(x)$d$x.


Dans le cas présent, les v.a. X1 et X2 ont une densité qui vaut 1 sur l'intervalle [0;1] et 0 ailleurs.
C'est une définition possible d'une loi uniforme sur [0;1].

On cherche la densité de S.
Dans la suite x est entre 0 et 1.
On a vu que
\text{P}(S_\alpha\le x)=\text{P}(X_1\ge\alpha\cap X_1\le x)+\text{P}(X_1\le\alpha\cap X_2\le x)
Comme X_1 et X_2 sont indépendantes

\text{P}(X_1\le\alpha\cap X_2\le x)=\text{P}(X_1\le\alpha)\times \text{P}(X_2\le x)=\alpha x
Comme la probabilité d'un intervalle est proportionnelle à sa longueur dans le cas d'une loi uniforme, on a
\text{P}(X_1 \leq x \cap X_1 > a)=\text{P}(a<X_1\le x)=\begin{cases}0 &\text{si } x\le a\\ x-a &\text{si } a\le x\le1\end{cases}

On en déduit que F_\alpha, fonction de répartition de S_\alpha, est définie par

\forall x\in\R\quad F_\alpha(x)=\begin{cases}0 &\text{si } x\in ]-\infty\,;0]\\\alpha x&\text{si } x\in [0\,; \alpha]\\\alpha x+x-\alpha&\text{si } x\in [\alpha\,;1]\\1&\text{si } x\in [1\,;+\infty[\end{cases}

Il est ensuite facile de dériver cette fonction pour avoir la densité de  S_\alpha .

Posté par
grenadine75re : Jeu de probabilités 19-02-17 à 11:41

Ah d'accord j'ai compris mon erreur comme x [0,1] je pensais qu'il fallait intégrer P(X1x) sur [0,1] et non comme une variable merci pour les explications détaillées.

Mais du coup est-ce que c'est normale d'avoir une densité supérieur à 1 sur [,1].

Par contre pour la question 2 j'ai du mal à comprendre le résultats qu'on doit obtenir.
La première partie de la question consiste à connaître la probabilité que le premier tirage de l'adversaire (en tant donné qu'il est au seuil zéro) soit inférieur à S , je ne comprend donc pas pourquoi X1 et X2 n'entre pas en compte dans le calcul?

Posté par
verdurinre : Jeu de probabilités 19-02-17 à 12:53

Il est normal d'avoir une densité supérieure à 1 sur [;1].

Ce que l'on doit avoir c'est \int_{\R}f_\alpha =1

Et dans notre cas
\int_{\R}f_\alpha =\int_0^\alpha \alpha$d$t+\int_\alpha^1(\alpha+1)$d$t=\alpha^2+1-\alpha^2=1
donc tout va bien de ce point de vue.


Pour la question 2).
Je ne vois pas comment la traiter sans faire la première partie de la question 3).
En désignant par Y la v.a. donnant le résultat du second joueur, la probabilité de gain du premier joueur est

p_1=\int_0^1 $P$(S_\alpha=x\cup Y<x)$d$x

Comme les tirages des deux joueurs sont indépendants, il vient
p_1=\int_0^1 $P$(S_\alpha=x)\times $P$( Y<x)$d$x=\int_0^1 f_\alpha(x)$P$( Y\le x)$d$x

Comme le second joueur rejoue systématiquement (seuil 0) Y suit une loi uniforme sur [0;1] et $P$( Y\le x)=x pour x entre 0 et 1.

Il faut donc trouver la valeur de qui maximise
\int_0^1 x f_\alpha(x)$d$x

Posté par
grenadine75re : Jeu de probabilités 19-02-17 à 13:55

Si mon raisonnement est bon \int_{0}^{1}{xf\alpha (x) dx}=\frac{1}{2}+\frac{\alpha }{2}(1-\alpha)
en étudiant les variation selon l'intégrale se maximise en =1/2 ?

Posté par
verdurinre : Jeu de probabilités 19-02-17 à 14:09

Je trouve le même résultat.

Posté par
grenadine75re : Jeu de probabilités 19-02-17 à 16:48

ok merci,

par contre à la question 3. pour le en déduire je n'arrive à déterminer d'où vient le terme  (²)/2 ...

Posté par
verdurinre : Jeu de probabilités 19-02-17 à 17:16

Pour la question 3 on calcule

p_1=\int_0^1 f_\alpha(x)$P$( S_\beta\le x)$d$x

avec $P$( S_\beta\le x)=\begin{cases}\beta x&\text{si }x\in[0\,;\beta]\\ \beta x+x-\beta &\text{si }x\in[\beta\,;1]\end{cases}

Comme on a par hypothèse

p_1=\int_0^\beta \alpha \beta x\,$d$x+\int_\beta^\alpha \alpha((\beta+1)x-\beta) \,$d$x+\int_\alpha^1 (\alpha+1)((\beta+1)x-\beta)\,$d$x

Ce qui, après quelques calculs,  donne bien le résultat demandé.

Posté par
grenadine75re : Jeu de probabilités 19-02-17 à 17:29

Super merci c'est vrai que je n'ai pensé à séparer les deux cas sur [0,]

Posté par
Ennydrare : Jeu de probabilités 20-02-17 à 14:27

Bonjour,

Merci bcp à tous pour vos réponses. J'en suis à la question 2, je n'arrive pas à maximiser l'intégrale...

J'ai trouvé \int_0^1 x f_{\alpha}(x) = \dfrac{\alpha+1-\alpha^2}{2}.

Pour maximiser, j'ai peut-être pas une très bonne méthode, je fais :

\dfrac{\int_0^1 x f_{\alpha+1}(x)}{\int_0^1 x f_{\alpha}(x)} = \dfrac{(\alpha+1)+1-(\alpha+1)^2}{\alpha+1-\alpha^2}... Puis j'essaye ensuite d'isoler quand 1 \leq \dfrac{(\alpha+1)+1-(\alpha+1)^2}{\alpha+1-\alpha^2} . Sauf que je trouve n'importe quoi en développant...

Comment faire ? J'ai l'impression de faire n'importe quoi ! Quelqu'un pourrait m'aider ?

Merci d'avance

Posté par
verdurinre : Jeu de probabilités 20-02-17 à 15:08

Bonjour,
le plus simple : 1+\alpha-\alpha^2=\frac54-(\frac12-\alpha)^2

Sinon on étudie les variations de la fonction

\alpha\mapsto \dfrac{\alpha+1-\alpha^2}{2}

sur [0;1] en la dérivant.

Posté par
Ennydrare : Jeu de probabilités 20-02-17 à 15:52

ah ben oui, avec la dérivée le résultat est très rapide... J'ai tendance à me compliquer la vie
Merci !!

Posté par
grenadine75re : Jeu de probabilités 20-02-17 à 19:14

Bonsoir,

j'aimerais savoir si ce calcul est juste pour la question pour qu'on est pas à passer par la question 3.

p1=\int_{0}^{1}{P(0\leq x\leq S\alpha )dx}
=\int_{0}^{1}{1-P( S\alpha\leq x )dx}
=\int_{0}^{\alpha }{(1-\alpha x) dx} +\int_{\alpha }^{1}{(\alpha -1)(1-x)dx}

car je finis par avoir le même résultat.

et pour la détermination de 2  j'ai fait l'hypothèse suivante;
soit g()= \dfrac{1}{2} + \dfrac{\alpha + \beta}{2}(1-\alpha-\alpha \beta)
g'()=\frac{\beta ²}{2}-\alpha \beta -\alpha +\frac{\beta }{2}+\frac{1}{2}
je suppose que pour maximiser p1, = du coup je trouve bien \alpha_2 = \dfrac{\sqrt{5}-1}{2}
mais si =,   p1=\frac{1}{2} ...

Posté par
verdurinre : Jeu de probabilités 20-02-17 à 19:56

Salut grenadine.
Ton calcul de p1 ne peut pas être juste : la valeur de n'y intervient pas.

Attention

\large p_1=\frac12+\frac12(\alpha - \beta)(1-\alpha-\alpha \beta)

Pour la suite, je ne comprend pas bien ton raisonnement.

Personnellement je suis parti de l'idée que la valeur à choisir doit être telle que l'autre joueur ne peut pas prendre un seuil plus grand sans diminuer ses chances de gain.

Il est par ailleurs évident que si les deux joueurs choisissent la stratégie optimale, leurs chances de gain sont égales.
Ce qui caractérise cette stratégie est que si l'autre joueur s'en écarte il diminue sa probabilité de gagner.

Posté par
grenadine75re : Jeu de probabilités 20-02-17 à 20:35

en faite si je suis parti du principe que si le joueur 2 est au seuil =0 on ne se préoccupe que du premier tirage Y1 qui doit être compris entre =0 et S mais c'est vrai que je trouve ça hazardeux même si on trouve le bon résultat ^^

Et pour 2 si =
g'()= \frac{1}{2}(-\alpha ²-\alpha +1) donc on a deux valeurs pour lesquelles g'()=0 sauf que l'une [0,1]
donc g() se maximiserai en 2.

mais si je suis votre raisonnement mon résultat reste juste nan?

Posté par
verdurinre : Jeu de probabilités 20-02-17 à 20:54

Je ne vois pas d'où vient g'().

Est-ce une dérivée ? Si oui, de quelle fonction ?

Le résultat est donné dans l'énoncé, on peut supposer qu'il est juste.

Posté par
grenadine75re : Jeu de probabilités 20-02-17 à 21:05

je l'ai mis plus haut  g()= \dfrac{1}{2} + \dfrac{\alpha - \beta}{2}(1-\alpha-\alpha \beta) (avec la correction)

Posté par
verdurinre : Jeu de probabilités 20-02-17 à 21:55

Dans ce cas g'(\alpha)=\frac12(1-2\alpha-2\alpha\beta +\beta^2).

En dérivant par rapport à .
Mais ceci ne permet de trouver la meilleure stratégie que si on connaît . (Et que 2)

Pour ton problème l'idée est plutôt de trouver une stratégie, c'est à dire une valeur de , telle que l'on soit certain d'avoir une probabilité de gain au moins égale à 1/2.
On ne peut pas faire mieux que 1/2, car si l'autre joueur utilise la même stratégie alors la probabilité de gain est 1/2.

Posté par
grenadine75re : Jeu de probabilités 20-02-17 à 22:55

J'avoue que je ne vois pas du tout où partir...

Posté par
verdurinre : Jeu de probabilités 21-02-17 à 10:44

Avec un peu de retard, pour illustrer mon raisonnement :

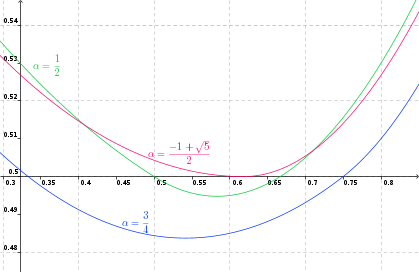
Jeu de probabilités

On a des courbes donnant la probabilité de gain ( en ordonnée )  d'un joueur choisissant le seuil en fonction du choix de l'autre joueur ( en abscisse ).

On peut voir que le choix de \alpha=\frac{-1+\sqrt5}2 garanti une probabilité de gain supérieure ou égale à 1/2 quelque soit le choix de l'autre joueur.
Ce qui n'est pas le cas pour les autres choix.

Posté par
grenadine75re : Jeu de probabilités 21-02-17 à 16:01

je comprend ton raisonnement en faite à l'inverse de moi tu as voulu savoir en quelle valeur p1 a le plus de chances de gagner mais le problème c'est que je ne vois pas comment prouver analytiquement ce résultat... en partant de g'()?

Merci en tout cas de nous avoir aider verdurin

Posté par
verdurinre : Jeu de probabilités 21-02-17 à 16:48

Mon idée repose sur la recherche du minimax .

Il est clair que la valeur du minimax est 1/2, par symétrie entre les joueurs.
Ensuite on regarde la probabilité de gain de celui qui joue le plus grand nombre.
Pour que l'autre joueur soit perdant en jouant un nombre plus grand il faut et il suffit que 1-- soit négatif pour .
D'où on tire que la valeur seuil vérifie 1--2=0.

C'est un peu confu, mais j'espère que cela vous servira.


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1675 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !