Inscription / Connexion Nouveau Sujet
Joli schéma 
.
J'ai regardé les configurations en parce qu'elles me semblaient éventuellement prometteuses pour un meilleur optimum que
. Mais pas du tout. Ce n'est pas ça qui prouve quoi que ce soit, mais du coup mon intuition à changé de camp
...
Je pense que tu as suivi le même raisonnement que moi...
Je pensais améliorer pour n=8, mais je n'ai pas réussi!
Pourtant, je pensais également qu'on pourrait améliorer...
Bonjour à tous,
Pour ma part, j'avais surtout voulu dire que je n'étais pas convaincu par la démonstration qui passait de condition suffisante à nécessaire abusivement.
Pour me faire comprendre, j'avais cherché à introduire un doute !
J'ai cherché (je cherche encore) à démontrer, par exemple par l'absurde, que "2n-3 est impossible", ce qui en complément de "2n-4 suffisant" bouclerait le dossier, mais, plus difficile à faire qu'à dire !
Profitons-en pour remercier les initiateurs de ces énigmes qui nous obligent à faire fonctionner nos cerveaux, au-delà de ce qu'ils s'imaginent, j'en suis persuadé.
J'ai cherché (je cherche encore) à démontrer, par exemple par l'absurde, que "2n-3 est impossible", ce
Merci de lire "2n-5" et non pas 2n-3...erreur grossière, mais vous aviez rectfié !
Mon idée est de remonter.
Si à l'issue du (2n-5) ème échange, tout le monde sait tout, nécessairement au coup d'avant on avait telle ou telle situation, donc auparavant ...pour arriver à un niveau où c'est manifestement impossible.
moi j'ai trouvé 11
mais apparemment la bonne réponse c'est 10
quelq un peux m'explique le truc de n-2
Il suffit de regarder les réponses de ceux qui ont obtenu un smiley, la solution qu'ils proposent résout le problème en 10 appels.
On peut démontrer facilement que pour n espions, on peut résoudre ce problème en 2(n-2) = 2n-4 appels, avec n
4.( voir post du 29/06/14 à 13h28, et celui du 01/07/14 à 20h03,
pour voir deux démonstrations différentes)
Pour 7 espions, on sait donc que l'on peut trouver des solutions pour 2(7)-4 = 10 appels
Sauf que l'on ne sait pas si ce résultat de 2n-4 appels est le minimum, la question est donc soit de démontrer que pour plus de 4 espions, on ne peut pas résoudre le problème en moins de 2n-4 appels, soit de trouver une solution en moins de 2n-4 appels, et dans ce cas, trouver une formule qui généralise ce minimum (si c'est possible).
quelqu'un peux m'expliquer le truc de n-2
Quand on cherche à généraliser le problème en considérant
Il suffit pour cela que dans un premier temps un agent appelle tous les autres pour collecter tous les secrets (donc
Dans ce cas on a bien les
Dans son post de du 01-07-14 à 20:03, weierstrass a montré une solution encore meilleure, qui garantit la distribution en
En procédant ainsi, il y a au total
... et on constate que les secrets sont intégralement distribués (parce que lorsque l'un des deux "agents appelants" (le n°
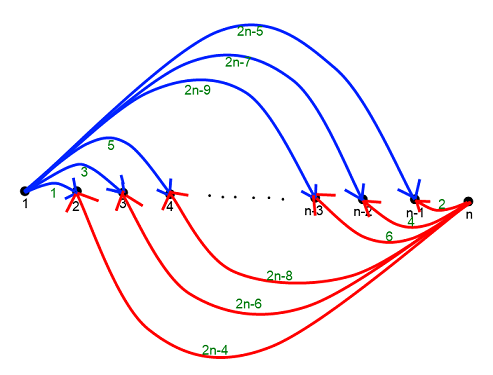
Voici le schéma des appels (avec l'ordre qui est important) :
La question qui demeure est la suivante :
Grâce à la solution directe de Wierstrass (ou grâce à une démonstration par récurrence comme celles qui ont été évoquées dans la discussion), on a la preuve d'une conjecture "faible", qui est que l'optimum est au pire égale à
Bonjour Weierstrass,
J'ai été interrompu dans la rédaction de mon message... que j'ai de ce fait posté en différé et "en aveugle", sans savoir que tu avais répondu entre temps ...
Quand on cherche à généraliser le problème en considérant n agents détenant chacun un secret, il existe une solution "naïve" c'est à dire très simple, qui permet de distribuer tous les secrets à tous les agents en N = 2n - 3 appels.
Il suffit pour cela que dans un premier temps un agent appelle tous les autres pour collecter tous les secrets (donc n-1 appels), puis dans un deuxième temps qu'il rappelle tout le monde (sauf le dernier appelé) pour "distribuer" l'intégralité des secrets (donc n-2 appels).
Dans ce cas on a bien les n secrets distribués aux n agents en N=2n-3 appels.
Dans son post de du 01-07-14 à 20:03, weierstrass a montré une solution encore meilleure, qui garantit la distribution en N = 2n-4 appels. Dans sa solution l'agent n°1 appelle les agents 2 à n-1. Et l'agent n appelle parallèlement et dans l'ordre inverse, les agents n-1 à 2.
En procédant ainsi, il y a au total N = (n-2) + (n-2) = 2n-4 appels...
... et on constate que les secrets sont intégralement distribués (parce que lorsque l'un des deux "agents appelants" (le n° 1 et le n°n) appelle un agent que l'autre a déjà appelé... tous les secrets sont mis en commun.
Nombre de participations : 0
0,00 %0,00 %
0Temps de réponse moyen : 120:22:15.
Annuler
connectez vous