Inscription / Connexion Nouveau Sujet
La dentelle de Sierpinski
Je vous propose un peu de beauté mathématique même si je n'arrive toujours pas à saisir l'ensemble des résultats 
Prenons un quadrillage et plaçons dans le coin inférieur gauche la valeur 1. Ensuite pour chaque case du quadrillage plaçons la somme des valeurs se trouvant en dessous ou à gauche de cette case.
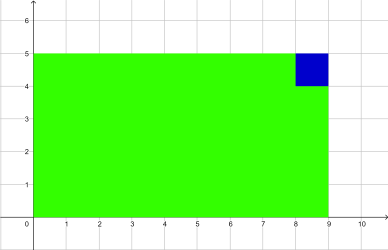
La case bleue (de coordonnées (8;4)) contient la somme de la surface verte
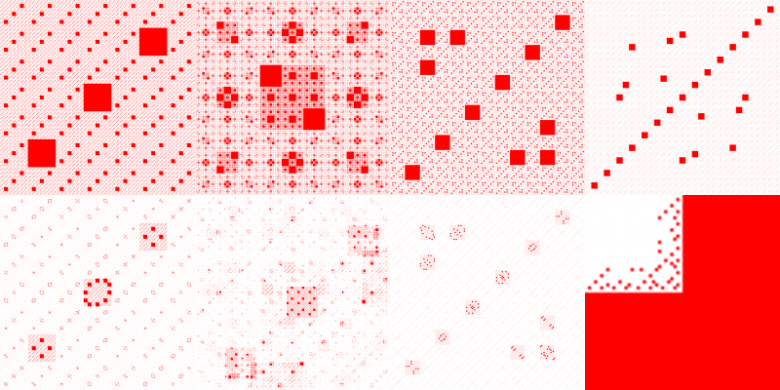
Ensuite choisissons un nombre entier positif m et colorons les cases qui contiennent les multiples de m. Il apparait des formes complexes et cependant très régulières. Par exemple pour m égal à 3, on obtient un tapis de Sierpinski
Il semblerait que pour tout m premier on obtient une fractale. Voici les images obtenues pour m = 7, 9, 13, 31, 45, 105, 169 et 232 (les échelles ne sont pas les même).
Soit la valeur de la case (x,y).
et
.
0) Montrer que est symétrique selon l'axe y=x.
1) Simplifier comme la somme de trois termes.
2) Prouver que si m est une puissance de 2 alors est multiple de m pour tout x plus grand qu'une limite. Donner cette limite.
3) Montrer que pour a et b premier entre eux alors la case (x;y) dans l'image pour m=ab ne sera colorée que si cette case est colorée pour l'image pour m=a et pour l'image m=b.
4) Montrer que si a est impair alors l'image pour m=2a est la même que celle pour m=a.
5) Donner une forme close pour ,
,
, ...
* A partir d'ici, je n 'ai pas les solutions *
6) En déduire une forme close pour .
7) Pour m premier, prouver que si est multiple de
alors
l'est aussi (
). Et que donc
est de nature fractale.
Voilà, en espérant que ça vous émerveille autant que moi. C'est fou ce que cette règle de base simple produit. J'ai passé pas mal de temps dessus et ça m'a fait replonger dans des mathématiques que je n'avais plus fait depuis longtemps. Les questions jusque 4) sont faciles, après ça se corse 
J'ai fabriqué un programme (en python ) pour générer les images donc si vous voulez une image particulière il suffit de demander 
Sinon après avoir répondu à la question 1) il est possible de créer les images dans Excel.
Oups, dans les images données, m = 7,9,13,31,49,105,169,232.
Les tailles des images avant compression sont 2401, 2187, 2197, 961, 2401, 2187, 2197 et 64 pixels de côté.
Bonjour,
et merci de nous faire chercher.
En allant sur Sierpinski vidéo,je suis tombé sur les 8 monstres (à voir absolument)
La trompette de Gabriel est particulièrement troublante car sa surface est infinie
et son volume fini.
Ce qui veut dire qu'on ne pourra jamais avoir assez de peinture pour la peindre ,mais
qu'on peut la remplir avec une quantité de peinture finie 
Bonsoir
LittleFox, je ne comprends pas ta construction.
"Prenons un quadrillage et plaçons dans le coin inférieur gauche la valeur 1. Ensuite pour chaque case du quadrillage plaçons la somme des valeurs se trouvant en dessous ou à gauche de cette case. "
Il n'y a rien en dessous ou à gauche puisqu'on part déjà du coin le plus en bas et le plus à gauche ! Peux-tu être plus explicite ?
Merci verdurin
C'est justement ce qui est troublant:
si on remplit un verre de peinture ses parois seront "peintes" (technique employée en
poterie ).
Dans la trompette de Gabriel ????
@derny
Il n'y a rien en dessous de la case du coin inférieur gauche, c'est pourquoi je lui donne une valeur arbitraire de 1. Pour toute les autres cases, on met la somme des case en dessous ou à gauche (ou les deux).
Toute case bleue, sauf (0;0), contient la somme des cases vertes.
Il y a une erreur dans la définition de . Évidemment
. Pour les autres cases,
.
@dpi Pour la trompette de Gabriel, pour en peindre la surface intérieur il faudrait mettre une peinture d'épaisseur nulle et donc le volume n'est pas défini ( 0 fois l'infini). De même pour la remplir il faudrait une peinture de viscosité nulle, sinon ça ne coulera pas jusqu'au fond et toute la surface ne sera pas peinte. Je ne vois pas de contradiction là dedans.
Bonjour. J'ai construit un tableau pour "voir" ce qui se passe.
x=y est évident du fait de la construction. J'ai des formules pour la diagonale et pour les 2 premières colonnes (ou lignes).
Je ne comprend pas quand tu dis que "la case bleue contient la somme de la surface verte".
Peux-tu donner les premières valeurs de ton tableau pour voir si elles correspondent aux miennes ?
@derny
Mon tableau commence comme ceci
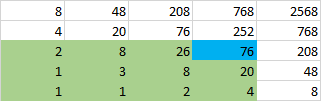
On voit que par exemple la case (3;2) en bleu contient la somme des cases en vert : 76 = 1+1+2+4+1+3+8+20+2+8+26.
Si tu as une formule pour la diagonale, ça m'intéresse. Ça ne m'a pas l'air évident
Je m'en doutais. Je n'avais pas compris comme il faut. J'avais compris que l'on additionnait les nombres dessus et les nombres à gauche. Ma deuxième colonne est 1, 2, 5, 12, …
Je dois tout reprendre.
Bonjour,
La diagonale semble progresser d'un coef 
10
Après 2568 on trouve: 26 928 , 286 048 , 3 002 816 ,32 717 952 , 328 220 288....
La formule reste à trouver
En fait j'ai trouvé une formule approximative pour la diagonale. Mais ça ne nous intéresse pas puisqu'on s'intéresse aux modulo .
La voici : pas simple
source :
Oui derny
J'avais un décalage après 26 928 ,mon tableau s'est révisé et je trouve comme sur la source de Littlefox.
@dpi
Le début de la figure pour m=3 ressemble à ça mais les valeurs ne sont pas bonnes. Les cases en jaune devraient contenir des multiples de 3. Compare avec le début de tableau que j'ai donné, ce n'est pas du tout les mêmes valeurs.
Astuce : sur Excel, la fonction MOD(n,m) permet d'éviter les nombres astronomiques puisqu'un nombre est multiple si son modulo est 0 et que le modulo de la somme est égal au modulo de la somme des modulo
Bonjour Littlefox,
Tu es un bon observateur et donc il ne t'a pas échappé que ces valeurs étaient le
résultat du quotient par 3.j'aurais pu afficher des X pour faire plus tapis 
Ça ne m'avait pas échappé du tout 
J'ai tellement joué avec des modulo que je ne m'attendais pas à voir de division .
Ça à l'air bon alors. Reste plus qu'à faire un tableau de 243x243 voir 2187x2187 pour bien voir la figure
Et il reste aussi à tester avec d'autres m 
Annuler
connectez vous