Inscription / Connexion Nouveau Sujet
Le jour des deux marchés
Bonjour , je vous propose l'exercice suivant ::
Dans une ville, deux marchés ont lieu à intervalles réguliers.
Le premier marché a lieu tous les 6 jours.
Le second marché a lieu tous les 9 jours.
On sait qu'un certain jour, les deux marchés ont lieu le même jour, et que ce jour est un mardi.
Quel sera le jour de la semaine du prochain jour où les deux marchés auront lieu en même temps ?
Bonjour à tous , La méthode PPCM(6,9) = 18 donne bien l'intervalle de temps entre deux coïncidences des marchés, mais elle ne permet pas à elle seule de déterminer le jour de la semaine.
Pour connaître le jour, il faut travailler modulo 7 en tenant compte du jour de départ.
Si l'on note les jours de la semaine modulo 7 (lundi = 0), le jour initial commun est mardi = 1.
Les jours du premier marché sont donc de la forme:
1 + 6k (mod 7)
Ceux du second marché sont de la forme :
1 + 9k′ (mod 7)
On cherche un jour commun J tel que
1 + 6k ≡ J (mod 7)
1 + 9k′ ≡ J (mod 7)
donc;
6k − 9k′ ≡ 0 (mod 7)
soit
2k − 3k′ ≡ 0 (mod 7)
La plus petite solution donne
J ≡ 3 (mod 7), c'est-à-dire un jeudi.
Le calcul ppcm seul ne suffit donc pas ici : il faut intégrer le décalage modulo 7. La bonne réponse est jeudi, pas samedi.
Bonjour,
Pour nous :
On sait qu'un certain jour, les deux marchés ont lieu le même jour, et que ce jour est un mardi.
c'est cette indication qui est le début de notre calcul.
@ flight,
Ta marche à suivre est bien trop compliquée.
Ma réponse en 3 lignes est complète et permet de trouver à coup sûr la réponse (Samedi)
PPCM(6,9) = 18 permet de connaître la "période" de répétition des jours communs.
On sait donc que le prochain jour commun sera 18 jours après le mardi
Comme dans 2 semaine (14 jours) on sera encore un mardi.
Dans 18 jours on sera 18-14 = 4 jours après un mardi.
D'où j'ai écrit : 18 = 14 + 4
qui permet de conclure : que le prochain jour "commun" sera un samedi
Si ta réponse est "Jeudi" ... et bien tu t'es trompé.
Illustration :
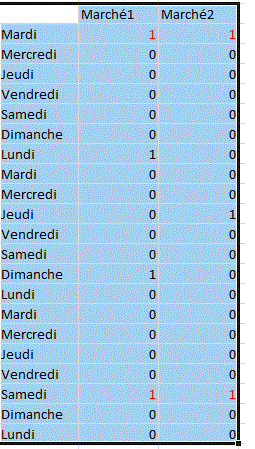
Peut-être, y a-t-il confusion sur l'expression "tous les 6 jours"
Si on dit tous les 7 jours, cela veut dire par exemple tous les mardis.
Donc si on dit tous les 6 jours, on doit décaler d'1 jour et donc si on part d'un mardi, le prochain sera un lundi et
le suivant un dimanche et ensuite un samedi et ...
C'est ainsi que la colonne 2 du tableau est faite.
Même principe avec "tous les 9 jours" qui donne la colonne 3 du tableau
Et on constate que c'est bien un SAMEDI que les 2 marchés seront synchrones en ayant commencé un mardi.
ma resolution etait pourrie , au depart on avait j=1+6k mod 7 et j= 1+9k' mod 7 on a donc 1+6k=1+9k' soit 6k=9k' ou encor 2k=3k' soit k=3p et k'=2p donc notre 6k donne 18p et j est donc de la forme 1+18p modulo 7 , si on prend p =0 on a mardi comme premier jour , si on prend p=1 , on a 19 modulo 7 qui donne 5 et le jour 5 c'est samedi en comptant depuis lundi(0)
L'arroseur arrosé 
Ca me fait du bien pour toutes les énigmes que tu poses et que je ne parviens pas à résoudre.
Surtout, continue! C'est grace à des abonnés comme toi que l'île continue de vivre et qu'on s'y amuse 


 Cliquez pour afficher
Cliquez pour afficher


