Inscription / Connexion Nouveau Sujet
les vecteurs 3
Bonsoir j'aimerais avoir une correction de mon exercice si il y a des erreurs , merci.
Soient A(-3; 1), B(6;4), C(3;-1) et D(13;2).
1. a. Calculer les coordonnées des vecteurs AB et CD.
b. ABCD est-il un parallélogramme ? Justifier.
2. Soit E(0;t) où t est un nombre réel.
a. Exprimer en fonction de t les coordonnées de AÉ.
b. Déterminer la valeur de t pour que le quadrilatère
ACBE soit un parallélogramme.
Voici mes réponses :
1. a.
Soit AB(xAB;yAB)
xAB = xB-xA = 6 -(-3) = 6 + 3 = 9
yAB = yB-yA = 4 - 1 = 3
AB(9;3)
Soit DC(xDC;yDC)
xDC = xD-xC = 13 - 3 = 10
yDC = yD-yC = 2-(-1) - 4 = 3
b. AB ≠ CD
Les vecteurs AB et CD ne sont pas égaux donc ABCD n'est pas un parallèlogramme.
2. a. A(-3;1) ; E(0;t)
Soit AE (xAE;yAE)
AE=(xE-xA;yE-yA)
xEA = (0-(-3) = 3
yEA = (t-1)
EA(3;t-1)
b. AC et BE
AC(xAC;yAC)
xAC = xC-xA = 3-(-3) = 6
yAC = yC-yA = -1-1 = -2
AC(6;-2)
BE(xBE;yBE)
xBE = xE-xB = 0-6 =-6
yBE = xE-yB = t-4
BE = t-4
t = -6 + 4 = -2
AC = BE
Les vecteurs AC et BE sont égaux donc ACBE est un parallèlogramme.
bonsoir,
question 1a) OK
1b) il doit s'agir de ABDC et non de ABCD, n'est ce pas ?
en effet, ABDC n'est pas un parallélogramme
2. EA ( 3 ; t-1), c'est vrai. mais on te demande EA, d'après l"énoncé.
ACBE est un parallélogramme si AE = CB
ou AC = EB
mais pas AC = BE..
reprends cette question
d'accord,
1. b. AB ≠ DC
Les vecteurs AB et DC ne sont pas égaux donc ABDC n'est pas un parallélogramme.
2. a. A(-3;1) ; E(0;t)
Soit AE (xAE;yAE)
AE=(xE-xA;yE-yA)
xEA = (0-(-3) = 3
yEA = (t-1)
EA(3;t-1) <= c'est ça EA non ?
oui, c'est EA, mais la question est ". Exprimer en fonction de t les coordonnées de AÉ", pas EA...
il est tard, je quitte.
A demain.
AC = EB
Les vecteurs AC et EB sont égaux donc ACEB est un parallèlogramme.
AC = EB quand t=-2 ?? non, c'est faux.
gabno,
ce que tu écris n'est pas clair.
tu me dis que tu veux écrire l'égalité AC = EB et tu calcules les coordonnées de BE ??
Tu confonds BE et EB
tu veux écrire l'égalité AC = EB
EB ( xB - xE ; yB - yE)
avec B(6 ; 4) et E(0 ; t) ca donne EB( ?? ; ?? )
et quelles sont les coordonnées de AC ?
d'accord,
AC = EB
EB ( xB - xE ; yB - yE)
EB (0-6) = -6 ; (0-(-3) = 3 = (t-1)
EB = t = -6/1 = -6
EB = -6
gabno,
je suis désolée de dire ça, mais tu écris n'importe quoi.. tu fais du copié collé de choses fausses ; et tu ne fais pas attention à ce que j'écris.
EB = -6 ça ne veut rien dire
EB ( xB - xE ; yB - yE)
avec B(6 ; 4) et E(0 ; t)
toi tu écris ensuite xEB = 0-6, soit xE - xB : tu inverses ! pourtant, c'est juste de la recopie.
xEB = xB - xE = 6 - 0 = 6 (et non -6) !
ensuite yEB = yB - yE = 4 - t ( pourquoi écris tu t-1 ? mystère !)
enfin tu n'as pas écris les coordonnées de AC ..
concentre toi, ce serait bien qu'on termine, là..
Désolé mais je peux te comprendre et merci pour tes bons conseils 
Les coordonnées de EB :
B(6 ; 4) et E(0 ; t)
EB ( xB - xE ; yB - yE)
xEB = xB - xE = 6 - 0 = 6
yEB = yB - yE = 4 - t
Les coordonnées de AC :
A(-3 ; 1) et C(3 ; -1 )
AC (xA - xC) ; (yA - yC)
xAC = xA - xC =-3 - 3 = -6
yAC = yA - yC = 1 - (-1) = 2
coordonnées de EB ( 6 : 4-t) oui, comme je te le disais
coordonnées de AC, tu les calcules encore une fois à l'envers.
AC ( xC - xA ; yC-yA) alors que toi, tu écris l'inverse (avec A d'abord).
tu dois bien te douter que tu fais erreur, puisque pour xEB et xAC tu devrais trouver la même chose..
donc AC ( xC - xA ; yC-yA)
AC ( 6 ; -2)
à présent
AC = EB ==> xAC = xEB c'est vrai
et yAC = yEB donne -2 = 4-t
==> t = ??
enfin, pour vérifier ta réponse, fais un schéma. As tu placé les points A, B, C, D dans le repère ?
maintenant que tu as calculé t, tu peux aussi placer E..
gabno,
non, ca ne fait pas t=-2
as tu fait le schéma ? quand tu places E(0 ; -2), tu obtiens un parallélogramme ACBE ?
je ne crois pas.
4 - t = -2
- t = -2 -4
- t = -6
t = 6
place E (0 ; 6) : que dis ta figure ?
je dis de la figure ACBE c'est un parallélogramme (je viens de le finir à main levée, je te montre ça)
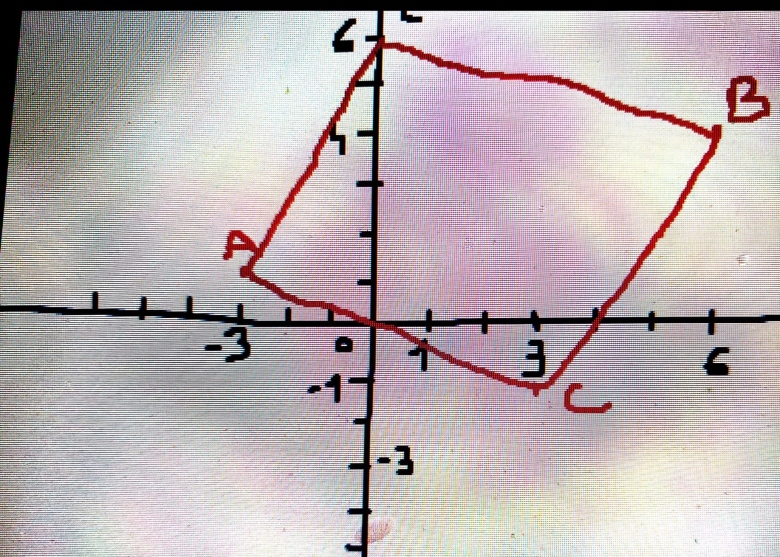
oui, c'est ça.
Un conseil : applique ton cours plus rigoureusement, fais une figure dès que c'est possible, même si ça n'est pas demandé et reprends les équations vues au collège, c'est indispensable.
Bonne soirée.
d'accord, merci beaucoup pour ton aide et tes conseils ils m'ont beaucoup aidé.
Résumons :
1. a.
Soit AB(xAB;yAB)
xAB = xB-xA = 6 -(-3) = 6 + 3 = 9
yAB = yB-yA = 4 - 1 = 3
AB(9;3)
Soit DC(xDC;yDC)
xDC = xD-xC = 13 - 3 = 10
yDC = yD-yC = 2-(-1) - 4 = 3
b. AB ≠ DC
Les vecteurs AB et DC ne sont pas égaux donc ABDC n'est pas un parallèlogramme.
2. a. A(-3;1) ; E(0;t)
Soit AE (xAE;yAE)
AE=(xE-xA;yE-yA)
xEA = (0-(-3) = 3
yEA = (t-1)
AE(3;t-1)
Les coordonnées de EB :
B(6 ; 4) et E(0 ; t)
EB ( xB - xE ; yB - yE)
xEB = xB - xE = 6 - 0 = 6
yEB = yB - yE = 4 - t
EB(6;4-t)
Les coordonnées de AC :
A(-3 ; 1) et C(3 ; -1 )
AC (xC - xA) ; (yC - yA)
xAC = xC - xA = 3 - (-3) = 6
yAC = yC - yA = -1 - 1 = 2
AC(6; -2)
b.
Si AC = EB
On a donc, xAC = xEB
yAC = yEB
On sait que AC (6; -2)
On sait que EB (6 ; 4-t)
Calculons t :
-2 = 4-t
4 - t = -2
- t = -2 -4
- t = -6
t = 6
La valeur de t pour que le quadrilatère ACBE soit un parallélogramme est de (0;6).


