[tex] \epsilon > 0, on  pose  \eta = \frac{1}{\epsilon}

Soit  x \in ]0  ,  \eta[

on a donc 0 < x < \frac{1}{\epsilon}

0  <  sin x   <  sin (\frac{1}{\epsilon})  <  1
et
\epsilon < \frac{1}{x}
[\tex]

comme sin(x)/x tend vers 1 quand x tend vers 0  , tu n'arriveras pas à montrer qu'il tend aussi vers 0

Bonjour ;

Montrons que \lim_{x\rightarrow 0^+} \dfrac{sin(x)}{x} = 1 .

Nous allons allons travailler dans

re-Bonjour ;

Je m'excuse : c'était une fausse manœuvre .

Montrons que

Nous allons travailler dans





Soit la fonction définie sur   par .

L'étude de cette fonction donne :

Il suffit d'avoir

donc il suffit d'avoir

On peut prendre : .

Pour montrer que on suit la même démarche

Bonjour

l'étude de cette fonction ? faite comment ? en utilisant la dérivée ? si oui, c'est une preuve qui se mord la queue : pour établir que sin' = cos et cos' = - sin, on utilise la fameuse limite ...

bonjour,
au voisinage de 0+
sin(x)<x<tan(x)  d'où xcos(x)<sin(x) et  donc cos(x)<sin(x)/x
comme sin(x)<x  sin(x)/x <1
en conclusion cos(x)<sin(x)/x<1 et on sait que lim cos(x)  =1  qd x tend vers 0

ce qui ne répond pas à la question d'origine (prouver en revenant à la définition de la limite)

alors en utilisant le DL de sin(x) en 0 et bricoler avec les
De toute manière il faut bien partir d'un définition de sin(x)  , par exemple utiliser

c'est pareil que passer par la dérivée, utiliser le dl : comment on établit le dl sans passer par la limite ?
la question de comment est défini sin x est en effet pertinente, avant de se demander si on peut montrer que cette limite est 1 en passant par les epsilon et les alpha .... ce serait bien que Mickadoss passe dire dans quel contexte il se place ?

Il ne reste plus que la méthode géométrique mais ne correspond pas à  "la définition formelle de la limite" que souhaite Mickadoss .  

On obtient les inégalités suivantes:

Si on ne veut pas tourner en rond :
   une  définition de sin(x)  ( pour x dans et même dans )  est :  
sin(x) est la somme de la sdtg   (-1)ⁿ⁺²x²ⁿ⁺¹/(2n+1)!  ( n )autrement dit la limite de la suite  n  x - x³/3! +........+ (-1)ⁿx²ⁿ⁺¹/(2n+1)!  
Pour rendre sin(x)/x - 1 petit il suffit de rendre   (x) := |x|²/3! +........+ |x|²ⁿ/(2n+1)! +.....  
Comme , pour x 0 ,  on a :  0 < (x) < x² exp(||x|) c'est assez facile .

On se mords la queue. Tant qu'on y est on étudie la fonction

Ni queue ni morsure !
La seule définition correcte  que je connaisse des applications cos et sin s'obtient à partir de la définition  de exp(z)  , pour z dans , comme étant
exp(z) : = _n zⁿ/n!  
On pose ensuite  cos(z) :=( exp(iz) + exp(-iz))/2 et sin(z)  :=( exp(iz) + exp(-iz))/2i
On en déduit les propriétés classiques .

Voir   , par exemple,  le livre de  J. Dieudonné  : Fondements de l'analyse moderne pages 200 , 2001 .

@etniopal,
Oui, mais et existent avant cette expression.  Là il n y a ni queue ni morsure mais œuf et poule.

cos et sin existent avant cette expression ?
Comment étaient elle définies ?  Proprement ?

il reste que si on définit sin et cos comme sommes de séries entières, donc comme limites, revenir aux epsilons et aux alpha pour avoir la limite de sinx / x = 1-x²/3 etc, c'est un peu étrange, non ?

Bonjour Razes !
Quand tu écris

Citation :

On obtient les inégalités suivantes:

Bonjour luzak,

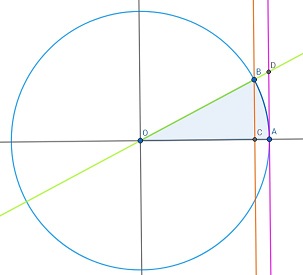
Pour ce qui est de l'escroquerie, la demonstration n'est pas de moi, voyons voir (utilisons la figure que j'avais poste):

Soit

Le cercle de rayon OA=1.






Nous avons

Il suffit de remplacer, on obtient:


Alors luzak, où est l'escroquerie?

Bonjour ;

d'après tes calculs Razes tu obtiens :

Il me semble que c'est plutôt que mais c'est un détail...

Tu as déplacé le problème en mettant des aires à la place des longueurs mais es-tu certain que le calcul de l'aire du secteur se justifie sans admettre que l'aire est proportionnelle à la mesure de l'angle ?  et cette mesure (en radians) demandant aussi un peu de trigonométrie !
Et aussi, je ne dis rien du "on voit que" pour l'inégalité des aires !

Même en l'état, c'est bon.

"faux  problème"

Dernier mot de ma part concernant cette chicane sans grand intérêt : la définition de la mesure en radians nécessite une définition correcte des lignes trigonométriques (en général venant de l'exponentielle complexe) et c'est la définition même de cette mesure qui donne la dérivée de la fonction usuelle sinus.