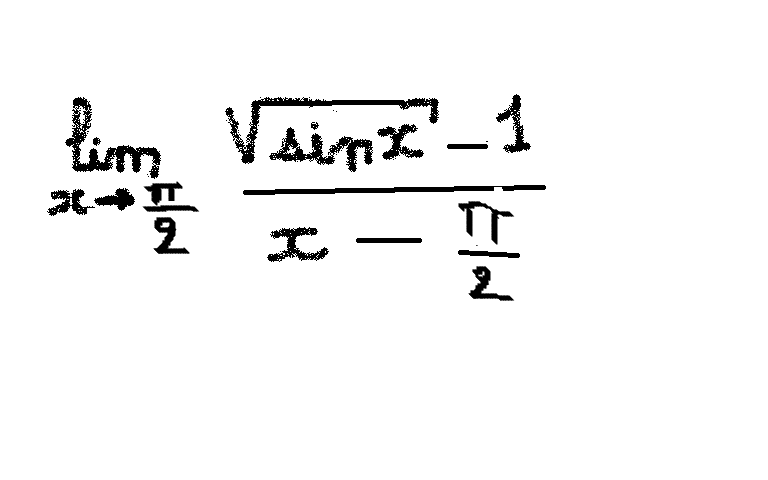
ça tend vers 0 : programme ta calculette en radians et introduit x=1,57, tu verras.

tu multiplies en haut et en bas par [racine(sinx) + 1] qui tend vers 2 lorsque x tend vers pi/2.
tu obtiens : (sinx - 1)/[(x-pi/2)*racine(sinx) +1]

tu poses X=x-pi/2 => x=X+pi/2 => sinx = sin(X+pi/2)=cos(X)
sinx - 1=cosX-1=-2sin^2(X/2) => sinx -1/X = -2sin^2(X/2)/X = -sin^2(X/2)/(X/2)

Qu'on peut aussi écrire : -sin(X/2)*[sin(X/2)/(X/2)].

Or X tend vers 0 lorsque x tend vers pi/2 et sina/a tend vers 1 lorsque a tend vers 0
donc sin(X/2)/(X/2) tend vers 1 lorsque X tend vers 0
donc (sinx - 1)/[(x-pi/2)*racine(sinx) +1] s'écrit : -sin(X/2)*sin(X/2)/(X/2)/[racine(sinx)+1] qui tend vers -sin(X/2)/2 lorsque X tend vers 0 puisque racine(sinx) +1 tend vers 2 lorsque x tend vers pi/2

Donc, je confirme que ta fonction tend vers 0 lorsque x tend vers pi/2

Je pense avoir trouvé la solution en associant l'expression conjuguée et le nombre dérivé.

A confirmer, merci !