Bonjour codos.

Par valeur supérieur, cela veut dire "par la droite". En prenant un point quelconque sur ton graphique, tu peux remarquer que tu peux approcher ce point par la gauche (par valeurs inférieures) ou par la droite (par valeurs supérieures).

Prenons 2. Par la gauche, cela serait 0.5 ; 1 ; 1.5 ; etc.
Par la droite, 3 puis 2,5...

Je dirais ceci :

Salut Fred !
"f(x) tend vers +infini quand x tend vers a"
quand on parle de  "f(x) tend vers +infini" : l'image de x tend vers + infini --> donc on parle de l'axe des ordonnées je ne me trompe pas en thermes de +infini.
et tout ça quand x tend vers a --> là c'est sur l'axe des abscisses ?

je ne sais pas si c'est clair, mais en tout cas merci pour l'histoire de droite/gauche c'est super sympas.

Quand tend vers , oui, c'est sur l'axe des abscisses.

peut être un réel dans l'ensemble de définition de ou peut ne pas l'être.

Exemple.

La fonction inverse :

Lorsque se rapproche de , sa limite se rapproche de l'infini.

Si on se rapproche de par la droite, c'est-à-dire par valeurs supérieurs (5, 4, 3, 2, 1...), la limite sera .
Si on se rapproche de par la gauche, c'est-à-dire par valeurs inférieurs (-5, -4, -3, -1, -1...), la limite sera .

Tu peux observer cela sur ce graphique.

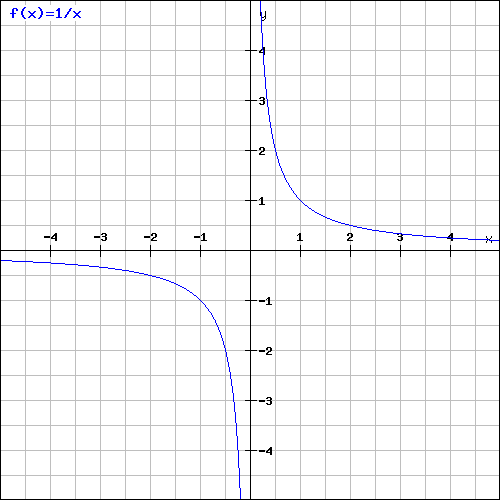
Et donc,

Lorsque x se rapproche de 0, sa limite se rapproche de l'infini.
-->ici on parle de l'infini car il y a une infinité de nombre avant d'arriver à 0 en quelque sorte ?

"Si on se rapproche de 0 par la droite, c'est-à-dire par valeurs supérieurs (5, 4, 3, 2, 1...), la limite sera +\infty."
-->on dit +infini car l'on est dans les nombres strictement positifs c'est à dire dans ]0;+infini[ ?

Même question pour
"Si on se rapproche de 0 par la gauche, c'est-à-dire par valeurs inférieurs (-5, -4, -3, -1, -1...), la limite sera -\infty."
--> L'on est dans les nombres strictement négatifs est donc ]-infini;0[ ?

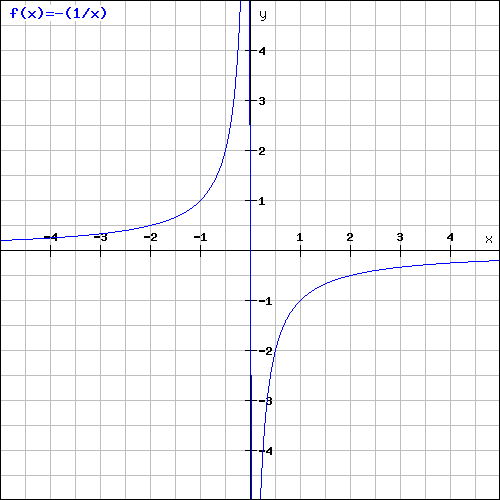
Ha mais OUI !! je viens de comprendre !!
donc par exemple pour la fonction -(1/x)
Si on se rapproche de 0 par valeur supérieur, alors la limite sera -infini.
Si on se rapproche de 0 par valeur inférieur, alors la limite sera +infini.

et donc, l'on dit ça comme ça ?
Lorsque x tend vers 0 par valeur supérieur, f(x) tend vers -infini
c'est ça ? ou cette phrase ne veut rien dire ?

Merci beaucoup Fred c'est super sympas !

C'est ça. On note :

  pour "valeur supérieure"
  pour "valeur inférieure"

Ou :







Ceci dit, il faudra justifier que cela soit ou par une étude de signe, cela vaut aussi pour des réels.

D'accord, merci beaucoup Fred, en fait j'essaye d'aborder un peu les limites, histoire d'avoir un peu d'avance étant donné que cette année et bien les maths c'est pas comme en seconde ou c'était très / trop simple.
Est ce que t'aurais un site ou justement on voit cette abord ? le 1er site que tu m'as passé, on évoque les asymptotes, ce que je ne connais pas du tout.

En tout cas un réel grand merci !!!

Bien que le chapitre s'appelle "Limite - Comportement asymptotique", les premières pages concernent bien les limites.

Quant au "comportement asymptotique", il arrivera par la suite.

Ok ok ! je vais attendre les explication du prof alors, en tout cas je te remercie beaucoup, c'est vraiment sympas !