Inscription / Connexion Nouveau Sujet
loi binomiale avec arbre
Bonjour,
voici un autre exercice à savoir :
Soit X la variable aléatoire qui suit la loi binomiale de paramètres n=3 et p=0,3, en vous aidant d'un arbre pondéré, déterminez la probabilité P(X=0), P(X=1) et P(X )
)
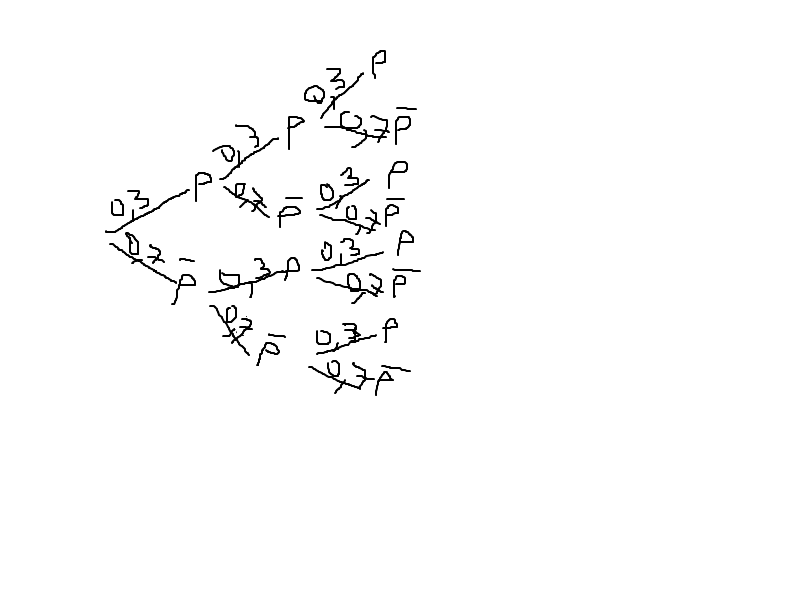
l'arbre que j'ai fait ai ci-dessous (pas beau mais je n'arrive pas à faire autrement sinon ça ne peut le prendre donc je suis allée le faire sur paint)
donc P(X=0)= 0,7*0,7*0,7=0,343
donc P(X=1)0,7*0,7*0,3=0,147
donc P(X 1)= je ne sais comment faire (peut-être prendre les deux valeurs ci-dessus et les diviser en 2) ?
1)= je ne sais comment faire (peut-être prendre les deux valeurs ci-dessus et les diviser en 2) ?
MERCI
Bonjour
ton calcul pour P(X=1) est faux
sur ton arbre, écris la valeur de X auxquelles correspondent chaque feuille de l'arbre
(les feuilles sont les noeuds finaux, qui n'ont plus de branche)
tu verras qu'il y a plusieurs chemins qui mènent à X=1
Re,
oui je suis d'accord qu'il y a plusieurs chemins mais pour moi je résultat était le même
je trouve trois fois la possibilité d'avoir P(X=1=
soit P P barre au dessus et P barre au dessus donc 0.3/0.7/0.7=0,147
et P barré au-dessus, P et P barré au dessus donc0.7*0.3*0.7=0,147
et P barré au-dessus P barré au-dessus et p donc 0.7*0.7*0.3=0,147
donc je dois répondre trois possibilité d'avoir P(X=1) c'est ça.
et pour P(X 1) ?
1) ?
et pour P(X=0) là je devais dire quoi alors (1 seule possibilité d'après l'arbre)
MERCI
S'il y a trois chemins pour mener à X=1, et que ces trois chemins sont bien disjoints, alors la probabilité de X=1 est la probabilité de l'union des trois chemins !
Pour P(X 1), tu peux remarquer que {X
1), tu peux remarquer que {X 1} = {X=1}
1} = {X=1} {X=0}
{X=0}
si on note A B et C les trois chemins, alors tu es bien d'accord que A B et C sont disjoints deux à deux (car si on n'a pris le chemin A, c'est qu'on n'a pas pu en prendre un autre, etc.)
Ensuite,
et que sait-on de la probabilité d'une union d'événements disjoints deux à deux ?
En fait, A B et C sont plutôt les événements correpsondant à "avoir emprunté tel chemin", pas les chemins en tant que tels
Re,
là je suis perdue complètement avec les trois chemins et avec mon arbre.
EN effet il y a 3 chemins pour avoir P(X=1) là ok
deux évènements A et B disjoints normalement c'est noté A B=
B=
après je ne sais pas
MERCI
Si deux événements A et B sont disjoints alors P(A union B) = P(A)+P(B)
Cela reste vrai si on a plus de 2 événements
Alors dans notre cas, A B et C sont disjoints 2 à 2
Donc que vaut P(A union B union C) ?
Bonjour,
@Zormuche
Je passe juste pour interroger sur le bien fondé de la présence des accolades dans
Re,
donc ici je me retrouve avec la même réponse que l'autre exercice
donc P(A) + P(B) + P(C)= 0,147+0,147+0,147= 0,441
ou la loi binomiale (3 parmi 1)*0,31*(1-0,3)3-1= 0,441
et pour P(X 1)
1)
Zormuche tu as écrit :
Pour P(X1), tu peux remarquer que {X1} = {X=1}{X=0}
que dois-je faire après (0,441* 0,343= 0,151263
MERCI
Re,
en faisant des recherches sur internet je pense qu'il fallait faire :
P(X 1)=P(X=1) +P(X=0) donc 0,441+0,343=0,784
1)=P(X=1) +P(X=0) donc 0,441+0,343=0,784
MERCI de me dire quoi




