Inscription / Connexion Nouveau Sujet
Lucie la puce
Bonjour, j'aurais besoin d'aide pour la question 2.
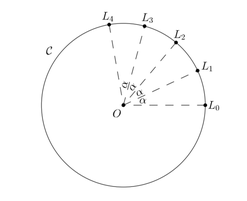
Enonce : Un terrain de sport a la forme d'un cercle C de centre O. A l'instant 0, Lucie la puce se trouve au point L0 de C. Chaque seconde, Lucie saute sur un autre point du cercle, decrivant successivement les points L1, L2, L3 etc. Lucie met toujours la meme force dans chaqye saut et saute toujours dans le meme sens, si bien que l'angle 
fait par deux points consecutifs avec le centre O de C est toujours le meme.
1) On pose =p/q (mesure en degres), ou p/q est une fraction irreductible. Combien de points differents Lucie va t-elle visiter ?
Si on divise par 360, on obtient une fraction. En faisant cette fraction irreductible, on trouve "p" nombre de tours et "q" nombres de points differents, pour que Lucie revienne a son point de depart. Donc "q" points differents.
2) Trouver deux angles =p/q et '=p'/q' tels que les points visites par Lucie selon l'angle soient tous differents de ceux visites selon l'angle ' (en dehors de L0).
Je bloque a cette question. Deja "en dehors de L0", si j'ai bien compris on parle du point de L0 et non du point a l'instant L0. Si je prends =120 et '=180, pour L3 de et L2 de ', on revient dans les deux cas sur notre point de depart. Donc ca ne marche pas. J'en suis parvenu que si on prend des rationnels, on reviendra toujours au point d'originie. Es ce que il serrait possible de mettre un irrationnel dans le couple p'/q', comme ca on obtiendra un angle irrationnel qui reviendra pas a son point de depart (question suivante). Par exemple: =360/2=180 et '=/2. Es-ce que ca pourrait marcher?
3)Existe-t-il un angle pour lequel Lucie ne reviendra jamais a son point de depart?
J'ai fais des recherches, et si l'on prend , un angle irrationnel, Lucie ne reviendra jamais sur son point de depart. Mais je sais pas trop comment l'expliquer.
Merci pour votre aide.
J'interprète autrement l'histoire de L0 dans la question 2).
Tout d'abord, tu as raison, le noter L0 perturbe.
Je propose de noter A le point de départ de la puce.
Dans 2), on veut que les points L' et L soient tous distincts sauf éventuellement A .
Plus précis : Avec E l'ensemble des points Lk et F l'ensemble des points L'k , on a A 
E et AF .
En effet L0 = L'0 = A .
Dans 2), on veut E
F = {A} .
Je vais regarder de plus près aussi la question 1). Je pense qu'il faut y parler de PGCD ou de PPCM pour exprimer p et q .
Avec mon interprétation, 120 et 180 répondent à la question 2). Si tu veux une "vraie" fraction, 120/7 et 180/11 marchent aussi.
Pour 1) en notant d le pgcd de p et 360, le nombre de points est q
360/d .
Remarque : Pourquoi niveau autre alors que tu es en terminale ?
salut
une chose m'échappe dans vos réponses 120 et 180° n'ont pas la forme p/q ou p/q est irreductible ....120° est obtenu en coupant le cercle en 3 et 180 en coupant en deux
Bonjour,
Pour la question 2, si j'ai bien compris il faudrai prendre pour denominateur alors tout les nombres entiers qui ne divisent pas 360? 7/11/13/... Mais on prend que les nombres premiers? Par exemple es-ce que on pourrait prendre 14, 14 ne divise pas 360 mais n'est pas premier. Apres comment on fait pour choisir le numerateur? Dans la question 2 on demande de trouver deux angles, vous avez trouve 120/7
17,14 et 180/1116,36, mais sont ils uniques? On pourrait prendre 120/1110,91 et 180/724,71. Apres ces deux angles reviennent sur L0, moi j'avais penser a prendre deux angles qui ont seulement L0 comme point en commun, d'ou l'idee de l'irrationnel qui ne reviendra pas a son point de depart (L0), mais un irrationnel ne peut pas s'ecrire sous forme fractionnaire ?
J'ai pas mis de niveau, car c'est un probleme qui n'est pas au programme. C'est un probleme de Benoit Rittaud.
Merci pour vos reponses 
L'énoncé ne le répète pas dans 2), mais il écrit " =p/q et '=p'/q' ". Pour moi il s'agit de 2 fractions irréductibles.
L'énoncé ne demande pas de trouver tous les angles, seulement d'en trouver 2.
Oui, 120/11 et 180/7 conviennent aussi.
" un irrationnel ne peut pas s'ecrire sous forme fractionnaire ? " : C'est la définition d'un irrationnel.
Un rationnel peut s'écrire sous forme fractionnaire, quotient de 2 entiers. Un irrationnel n'est pas un rationnel.
Qui est Benoit Rittaud ?
Exucsez moi, pour les reponses lentes, j'etais en voyage.
D'accord pour l'enonce de la question 2. Mais comment vous faites pour trouver vos numerateurs et denominateurs. Pour les denominateurs ont choisit des nombres qui ne divisent pas 360 c'est ca? Mais pour les numerateurs, on prend n'importe qu'elle rationnel?
Dans le cadre d'un projet en mathematiques, on devait choisir un probleme donne par un chercheur en mathematiques, dont Benoit Rittaud.
Annuler
connectez vous