Inscription / Connexion Nouveau Sujet
Manhattan robot
Bonjour à tous,
J'aimerais proposer cet exercice qui prolonge long fil 
Points acceptables . Il n'est pas utile de lire complètement les échanges du lien pour aborder cette nouvelle question .
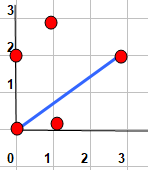
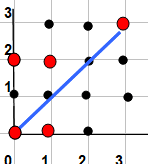
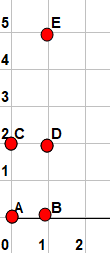
On considère des points aux noeuds d'un quadrillage orthonormé . La distance entre ces points est la distance Manhattan , c'est-à-dire la distance minimale parcourue par une personne allant d'un point à un autre en suivant les rues et les avenues . Par exemple la distance entre les points (1,3) et (3,0) est 5=2+3 . Contrairement à la distance classique du plan , le chemin minimal allant d'un point à l'autre est rarement unique . Maintenant , un peu comme dans le fil précédent , le diamètre d'un ensemble de points est la plus grande distance entre deux d'entre eux . On cherche le diamètre minimal d'un de ces ensembles qui contient n points mais aucun triangle isocèle ( attention , avec cette distance , les triangles isocèles sont curieux , par exemple ABC avec A(0,0) , B(3,0) et C(1,2) est isocèle en A ) .
Pour ceux qui préfèrent le concret , on a n robots situés aux carrefours d'une ville régulièrement quadrillée . Chacun est programmé pour rejoindre n'importe lequel de ses partenaires en limitant la longueur de ses déplacements . Donner la distance minimale séparant les robots les plus éloignés si initialement aucun d'entre eux n'est à la même distance de deux autres .
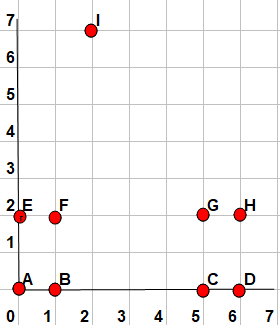
Par exemple avec n=4 le diamètre minimal est d(4)=3 comme le montre l'exemple ci-dessous :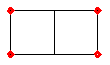
On s'amuse sans abuser du blankage ?
Imod
* Sylvieg edit> Je me suis autorisée à corriger une petite faute d'orthographe 
*
La faute devait être horrible mais je ne vois plus grand chose sur mon écran et je relis trop peu mon orthographe , j'essaie avant tout d'être clair . L'horrible faute a été corrigée , c'est l'essentiel 😊
@Dpi : d(5)=5 , pourquoi pas mais comment savoir si tu as compris si tu ne donnes pas d'explication ?
Imod
Vu:
Il faut aussi appliquer la distance manhattan pour tous les points
donc une diagonale 1x1 ne vaut pas 
2 mais 2
C'est ça , on doit suivre les lignes du quadrillage comme Trump qui déambulerait bêtement dans Manhattan sans savoir où il va 
Imod
Effectivement, mon programme pour Points acceptables peut être facilement modifié
Il n'y a qu'une seule solution pour d(4)=3 qui est bien le minimum.
Il y a 4 solutions pour d(8)=8. L'une est basée sur la solution de d(4).
Et à partir de ces solutions on peut retirer n'importe quel sommet pour atteindre le minimum de d(7) = 8 (11 solutions minimales).
On peut retirer 2 sommets de d(8) pour atteindre d(6) = 7 qui est le minimum.
On peut faire un peu mieux pour d(5) = 6 (10 solutions), les solutions sont plus ésotériques.
d(9) est plus difficile avec 27 solutions minimales mais un saut à d(9) = 12.
Je vous laisse chercher les figures
Je cherchais des solutions symétriques pour d(9) , j'avais presque renoncé et pourtant c'est tout bête : (0,0),(0,2),(0,3),(4,0),(4,2),(4,3),(9,0),(9,2),(9,3) .
J'ai regardé dans l'OEIS la suite n'existe pas , du coup je me suis demandé ( surtout pour LittleFox ) si on ne pouvait pas chercher les plus petits diamètres lorsque l'exigence est plus stricte à savoir que les distances entre deux points de l'ensemble doivent toutes être distinctes . On a un peu plus de chance que cette suite figure dans la bible des suites entières
Imod
Non, |(0,0)-(4,2)| = |(4,2)-(9,3)|=6
Mais bien essayé
Les solutions pour d(9)=12 n'avaient pas l'air très régulières. Après je n'ai pas analysé les 27 solutions 
Mince 
Au moins un côté positif , je ne suis pas un robot . Je n'aime pas trop me planter mais ça ne m'empêche vraiment pas de dormir
Y a quelque chose qui cloche là-dedans , j'y retourne immédiatement .
Imod
>Imod
Bonjour en partant de ta solution d(4) j'étais partie sur une extension pour d(8) mais je n'ai pas continué comme ta solution du 30 à 8h02 car je pensais qu'il fallait un mini unique (DE=AH ) si on nomme les ponts dans 'ordre de l'alphabet.
Sinon j'avais d(9)
Dans la variante que j'ai proposée on a d(1)=0 , d(2)=1 , d(3)=3 , d(4)=6 je me demande si on n'a pas ?
Pour 4 points on a par exemple (0,0),(1,1),(1,2),(5,1) .
Il est amusant de regarder la forme des cercles et de médiatrices avec cette distance
Imod
Voici toutes les solutions pour n=1..8:
Cliquez pour afficherEt pour n=9:
Cliquez pour afficherd(10) <= 13:
Cliquez pour afficherDans la variante que j'ai proposée on a d(1)=0 , d(2)=1 , d(3)=3 , d(4)=6 je me demande si on n'a pas
...
Imod
En tout cas c'est une borne inférieure par définition. Il faut voir après si c'est réalisable.
Oui , dans les premiers exemples on épuise les premières distances possibles et il serait intéressant de voir si on peut rester sur ce modèle . Pour 4 points , j'ai tracé les cercles de rayon 3 centrés sur les points de la position à 3 points , j'ai ensuite éliminé tous les points dans ces disques . Après on regarde un par un les points les plus proches de la frontière de la zone interdite et on supprime ceux qui sont à égale distance de deux des points précédents . A priori , il n'y a aucune raison que cette approche soit la bonne .
Imod
d(10) = 13
Cliquez pour afficherEt d(11) <= 15
[(0, 0), (1, 0), (-2, 0), (0, 3), (0, 4), (8, 0), (9, 0), (8, -2), (11, 0), (8, 4), (9, 4)]Pour être clair , quand je parle de cercle , il s'agit de cercle pour la distance Manhattan , c'est à dire de carrés usuels centrés sur le quadrillage et dont les diagonales en suivent les lignes .
Imod
Oui 
Pour le problème avec toutes les distances unique, il n'y a pas de solutions pour d(5)=10, le minimum est d(5) = 11
Par exemple:
{(0, 0), (0, 1), (0, 3), (1, 8), (4, 0)}Mais d(6) = comb(6,2) = 15
Par exemple:
{(0, 0), (1, 0), (-2, 0), (0, -5), (4, -5), (11, -2)}21 <= d(7) <= 22:
[(0, 0), (1, 0), (-2, 0), (0, -4), (0, 7), (-6, -8), (-14, 4)]28 <= d(8) <= 29:
[(0, 0), (1, 0), (-2, 0), (0, -4), (0, 7), (10, -4), (-12, -7), (0, -22)]36 <= d(9) <= 38:
[(0, 0), (1, 0), (-2, 0), (0, -4), (0, 7), (-11, -1), (-9, 13), (-21, -8), (-29, 5)]Il y a une incertitude sur d(n>6) car ça devient difficile d'explorer toutes les solutions.
Bon après plus d'une heure de calcul, je n'ai toujours pas prouvé d(11).
Et pour la version avec les distances uniques (appelons la u(n) pour éviter les confusions), j'ai juste 45 <= u(10) <= 48.
La force brute a ses limites
Il n'y a pas d'obligation de résultat , les premières valeurs éliminent certaines mauvaises pistes et c'est déjà bien . Après si le problème n'a pas d'intérêt concret comme par exemple de faire intervenir un robot proche d'un carrefour accidenté , il ne risque pas de motiver beaucoup de monde . Mais bon ici on s'amuse
Imod
salut
ce n'est pas qu'il ne m'intéresse pas ... mais c'est une question (comme la précédente) qui devient vite tempsgivore avec le nombre de points et par nature algorithmique : on place un point puis on vérifie les contraintes et soit on déplace le point soit on recommence lorsqu'il convient ...
j'ai donc suivi et encore plus quand je vois LittleFox intervenir car j'apprends beaucoup sur python avec lui (et même si je ne retiens ou comprends pas tout je l'en remercie) et je ne suis certainement pas capable de produire un script suffisamment efficace pour résoudre un tel pb ...
et je te remercie aussi pour ces pb que je trouve intéressant intellectuellement, et je trouve que ça c'est tout aussi important ...
Il m'arrive aussi régulièrement de suivre des sujets sans intervenir car je n'ai rien d'intéressant à ajouter et que je préfère me taire . Les exercices scolaires on en a tous mangé jusqu'à la nausée ( pour la bonne cause ) mais ici on est là pour s'interroger et s'amuser avant d'aller dans le trou
Je ne fais pas de hiérarchie , nous apprenons tous les uns des autres même si on a forcément nos préférences , on aime plus ou moins .
Merci pour ton compliment
Imod
Annuler
connectez vous