- Les nombres complexes - supérieur
- Nombres complexes : les classiques
- Équations différentielles : un Cours complet avec des exemples
- Ensemble et application Partie II
- Espaces vectoriels et Applications linéaires - supérieur
- Généralités sur les matrices, applications linéaires, changement de base, rang d'une matrice - supérieur
- Ensemble et application Partie I
Inscription / Connexion Nouveau Sujet
Nombres complexes - Lieux géométriques
Bonjour,
je voudrais avoir vos lumières sur un exercice qui me perturbe :
« 1.14. Déterminer le lieu des points d'affixe z tels que les points d'affixe z³, az², a²z forment un triangle équilatéral. »
J'ai procédé de la manière suivante :
1) D'une part, si z³=az²=a²z, alors le triangle est équilatéral et ce cas est possible si et seulement si a=0 ou z=0.
Ensuite, j'ai tenté avec la formule classique AC/AB = e ^ +- iπ/3 mais cela ne m'a rien donné... Après avoir cherché un bon moment, j'ai regardé la correction et elle utilise le fameux j = e ^ 2ikπ/3.
Je voulais savoir comment faire à partir de ce j et également comment le correcteur peut-il écrire « (z + a) / a = -j² soit finalement z = aj ».
Je vous remercie d'avance chers passionnés !
Jordane - www.cl4dou.net
Bonjour,
La méthode de lycée me semble pourtant fonctionner.
Si je pars de (un autre cas avec -pi/3 doit aussi être considéré), j'aboutis à
Justement, ce de quoi vous partez, ce n'est pas AC/AB mais CA/CB. Comment savez-vous qu'il faut tourner la formule dans ce sens pour avoir un résultat raisonnable à l'arrivée?
De plus, comprenez-vous pourquoi le correcteur peut-il écrire « (z + a) / a = -j² soit finalement z = aj » ?
Merci d'avance !
Jordane - www.cl4dou.net
Dans l'expression du rapport, un point apparaît deux fois (le centre de la rotation).
J'ai choisi pour ce point celui de puissance en z la plus faible.
Mais, quel que soit celui que tu retiens, cela devrait fonctionner. Montre tes calculs...
Concernant ta 2ème question, n'oublie pas que 1+j+j²=0
Cependant, ce résultat ne me convient guère : d'une part, car je n'utilise pas l'expression J qu'il me paraît important de savoir maîtriser en sup' ; d'autre part, la lourdeur de l'expression et son manque de synthèse m'empêcherait sûrement de le réutiliser si le pb était plus long.
Mais en fait, l'utilisation de ce fameux J n'est possible que si l'on considère dans le Plan de Gauss z³=1 pour dire z = e ^ (2ikπ/3), n'est-ce pas?
Partons de ton résultat...
Rappelons les propriétés de j :
j3=1
1+j+j²=0
De plus :
Revenons à nos calculs...
Le -j² s'obtient peut-être en prenant -pi/3 au début

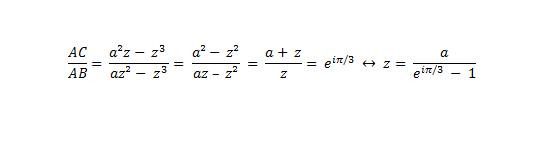

 analyse complexe en post-bac
analyse complexe en post-bac