Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... LicenceMaths 2e/3e a TopologieTopics traitant de topologie [tout]Lister tous les topics de mathématiques
Niveau LicenceMaths 2e/3e a
Partager :

Norme

Posté par
pfff 23-11-22 à 18:28

Bonsoir, je n'arrive pas à résoudre cet exercice. Merci de m'aider

Soient E le R-espace vectoriel des applications continues de [0; 1] dans R que l'on munit de la norme                     ∥f∥∞ = |f(x)|          
      supx∈[0,1]

et  L : E , f \int_{0}^{1}{f(t)dt}

1. Montrer que L est une forme linéaire continue de E dans R, et déterminer  sa norme N(L).

2. Soit F le sous-espace vectoriel de E constitué des applications de E nulles en 0, que l'on munit de la restriction de ∥ ∥∞ à F . Justifier que L|F est continue, et déterminer sa norme N(L|F ).


MES REPONSES

1- L est une forme linéaire
De plus \mid L(f) \mid \leq \int_{0}^{1}{\mid f(t)\mid dt }
                                   \leq \int_{0}^{1}{\mid \mid f\mid \mid _{\infty }dt}
                                   \leq \mid \mid f\mid \mid _{\infty }

Ainsi L est continue

On a donc N(L) 1

je n'arrive pas à déterminer la norme en sachant bien sur qu'elle fera 1

Posté par
pfffre : Norme 23-11-22 à 18:31

Désolé, Il y'a eu un décalage    \mid \mid f \mid \mid _{\infty } = sup \mid f(x)\mid
                                                          x [0,1]

Posté par
carpediemre : Norme 23-11-22 à 19:13

salut

1/ et si tu prenais la fonction constante f(x) = 1 et calculais ||L(f)|| ?

Posté par
pfffre : Norme 23-11-22 à 22:40

Comment je dois calculer vu que je ne connais pas l'expression de  ||.||  

Posté par
pfffre : Norme 23-11-22 à 22:51

Pour f : x1  , ||f||_{\infty } = 1 et L(f) = 1

Posté par
pfffre : Norme 23-11-22 à 22:52

comment déterminer maintenant ||L|| mais dans l'exercice noté N(L)

Posté par
elhor_abdelali Correcteurre : Norme 23-11-22 à 23:05

Bonsoir pff


je me permets de répondre vu que carpediem (que je salue) est déconnecté



Comme tu l'as bien vu on a pour tout f\in E, \Large\boxed{|L(f)|\leqslant||f||_{\infty}} et donc \Large\boxed{N(L)=\sup_{f\in E-\{0\}}\frac{|L(f)|}{||f||_{\infty}}\leqslant1}



et on a si on note f_0 la fonction constante sur [0,1] de valeur 1,


\Large\boxed{|L(f_0)|=\left|\int_0^1f_0(t)dt\right|=\int_0^1dt=[t]_0^1=1\leqslant N(L).||f_0||_{\infty}=N(L)}.


On conclut alors que \Large\boxed{\red{N(L)=1}}. sauf erreur de ma part bien entendu

Posté par
pfffre : Norme 24-11-22 à 15:11

Merci beaucoup elhor_abdelali j'ai très bien compris

Posté par
pfffre : Norme 24-11-22 à 15:17

Pour la 2e question déjà L|F est continue comme restriction d'une fonction continue
Mais comment ici je dois procéder pour determiner sa norme

Posté par
elhor_abdelali Correcteurre : Norme 24-11-22 à 19:55

Eh bien ici c'est un peu plus subtile


On a toujours pour tout f\in F, \Large\boxed{|L(f)|\leqslant||f||_{\infty}} et donc \Large\boxed{N(L|_F)=\sup_{f\in F-\{0\}}\frac{|L(f)|}{||f||_{\infty}}\leqslant1}


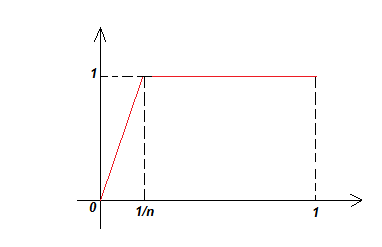
pour voir que l'on a aussi \Large\boxed{N(L|_F)\geqslant1} (remarquer que f_0\notin F) on peut considérer (par exemple) la suite de fonctions (f_n)_{n\geqslant1} :


\Large\boxed{f_n(x)=\left\lbrace\begin{array}l nx~~,~~0\leqslant x\leqslant\frac{1}{n} \\ 1~~,~~\frac{1}{n}\leqslant x\leqslant1 \end{array}}

Posté par
elhor_abdelali Correcteurre : Norme 24-11-22 à 20:54

Comme tu peux le voir on a bien \Large\boxed{\forall n\geqslant1~,~f_n\in F} et \Large\boxed{||f_n||_{\infty}=1}

et un calcul simple donne \Large\boxed{\forall n\geqslant1~,~L|_F(f_n)=1-\frac{1}{2n}}

et donc \Large\boxed{\forall n\geqslant1~,~N(L|_F)\geqslant1-\frac{1}{2n}} d'où le résultat par passage à la limite. sauf erreur de ma part bien entendu

Norme

Posté par
elhor_abdelali Correcteurre : Norme 24-11-22 à 21:07

remarque : on peut montrer que cette norme n'est pas atteinte


c'est à dire qu'on ne peut pas trouver de f\in F telle que, ||f||_{\infty}=1 et |L|_F(f)|=1.

Posté par
pfffre : Norme 28-11-22 à 09:22

Je ne comprends pas bien .

Si fn F alors elle doit être nulle en 0. Mais elle vaut 1 sur un certain intervalle

Et aussi je n'arrive pas à trouver L|F(fn)

Posté par
pfffre : Norme 28-11-22 à 13:15

Pour la 1ere préoccupation ca va jai capté mais pour la 2e pas encore

Posté par
GBZMre : Norme 28-11-22 à 13:48

Bonjour,
Vraiment, tu ne sais pas calculer \int_0^1f_n(t)\,dt pour le f_n défini par elhor_abdelali, dont il a dessiné le graphe plus haut ,


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1674 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !