Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... LicenceMaths 2e/3e a ProbabilitésTopics traitant de probabilités [tout]Lister tous les topics de mathématiques
Niveau LicenceMaths 2e/3e a
Partager :

Paramètres convergence en loi vers une loi normale

Posté par
Kernelpanic 20-05-20 à 17:50

Bonsoir à tous,

je bloque sur un sujet d'annale de probabilités :

"Soit (X_n)_{n \geq 1} une suite de variables aléatoires i.i.d suivant une loi de Poisson de paramètre 1. Déterminer deux constantes a et s telles que :

\dfrac{X_1^2 +\dots + X_n^2 - na}{s} \Rightarrow \mathcal{N}(0,1 )"

J'ai pensé au départ à utiliser le théorème central limite, mais pas de racine de n au dénominateur. J'ai donc pensé à la faire apparaître en multipliant par ci par là des quantités pour ensuite utiliser Slutsky mais rien (et je n'arrive pas à calculer la variance du carré d'une loi de poisson surtout...). J'ai ensuite pensé au théorème de Levy sur la convergence des fonctions caractéristiques, mais là non plus j'arrive pas à déterminer la fonction caractéristique du carré d'une loi de poisson de paramètre 1. La théorème central limite me plaisait bien, car "s" ça ressemble pas mal à "sigma" et "a" average (même si c'est pas le terme employé en anglais je crois). Auriez-vous une piste ?

Merci.

Posté par
WilliamM007re : Paramètres convergence en loi vers une loi normale 20-05-20 à 18:23

Bonjour Kernelpanic

Pourrais-je connaître le sujet dont c'est tiré ? Il y a clairement un problème.

Par la loi forte des grands nombres, on a nécessairement a=\mathbb E[X_1^2], sinon le rapport tend clairement presque sûrement vers +infini, ou -infini.

D'autre part, en notant \sigma l'écart-type de X_1^2, on a

\frac{X_1^2 +\dots + X_n^2 - na}{s}=\frac{X_1^2 +\dots + X_n^2 - na}{\sigma\sqrt n}\frac{\sigma\sqrt n}{s}.

Le premier facteur converge par le TCL vers la loi normale centrée réduite, et le second converge presque sûrement vers +infini. Par Slutky, le rapport converge en loi vers la variable aléatoire qui vaut +infini avec proba 1/2 et -infini avec proba 1/2. Il y a donc selon moi un problème d'énoncé.

Posté par
Kernelpanicre : Paramètres convergence en loi vers une loi normale 20-05-20 à 18:34

Bonjour WilliamM007, merci de la réponse  ! C'est un sujet de l'année 2017 de ma fac que j'ai reçu par mail pour nous entraîner, si tu me dis qu'il y a une coquille je vais demander à mon prof sur le champ (il a peut-être oublié de la corriger ou de la mentionner dans le mail). Je reviens très bientôt avec la réponse (demain normalement). Tu penses qu'en rajoutant un racine de n au dénominateur, on peut faire quelque chose ? Je vois pas trop comment calculer la variance de X1^2 à vrai dire...

Posté par
verdurinre : Paramètres convergence en loi vers une loi normale 20-05-20 à 18:35

Bonsoir,
il y a une erreur : la variance de X_1^2 +\dots + X_n^2 est n fois la variance de X^2 qui n'est pas nulle.

Je pense que le \sqrt{n} au dénominateur a disparu à la suite d'une faute de copie.

Posté par
Kernelpanicre : Paramètres convergence en loi vers une loi normale 20-05-20 à 18:42

Bonsoir verdurin, merci, ça a l'air de bien confirmer qu'il manque un racine de n... je vais me remettre aux calculs pour voir comment calculer la variance.

Posté par
Kernelpanicre : Paramètres convergence en loi vers une loi normale 20-05-20 à 18:47

Je crois qu'en réalité le calcul n'est pas très compliqué si on repart de la définition de la variance (et non pas du calcul simplifié où l'on fait intervenir le moment d'ordre 2 et le carré de l'espérance !). Je vérifie.

Posté par
Kernelpanicre : Paramètres convergence en loi vers une loi normale 20-05-20 à 18:56

Mh finalement je pensais pouvoir jouer sur le fait que l'espérance de X1 était égal au carré de son espérance pour faire apparaître la variance etc... mais non.

Posté par
Kernelpanicre : Paramètres convergence en loi vers une loi normale 20-05-20 à 22:58

Bon, je sèche sur la variance de X^2. Je retente demain.

Posté par
WilliamM007re : Paramètres convergence en loi vers une loi normale 20-05-20 à 23:27

Kernelpanic @ 20-05-2020 à 22:58

Bon, je sèche sur la variance de X^2. Je retente demain.

Il y a une astuce bien connue pour calculer les moments d'une loi de Poisson. Remarque que pour tout k\in\N^*,
\mathbb E[X(X-1)\cdots(X-k)]=1.

Tu en déduis de proche en proche les moments. Personnellement je trouve \operatorname{var}(X_1^2)=11.

Au passage, pour qu'on soit vraiment convaincus que l'exercice est erroné, j'ai fait des simulations. À gauche, le ratio de l'exercice. Chaque couleur correspond à une simulation différente, partant de n=0 à n=10^6. On voit bien que dans la moitié des cas, elles prennent des grandes valeurs positives, et dans l'autre des grandes valeurs négatives. À droite, c'est l'histogramme du ratio correctement renormalisé, c'est-à-dire avec a=2, s=racine(11) et un facteur en racine(n) au dénominateur. Au lieu de regarder les trajectoires, j'ai tracé l'histogramme, et l'ai comparé avec la densité de la loi normale centrée réduite (en rouge). Je pense qu'il n'y a pas de doute...

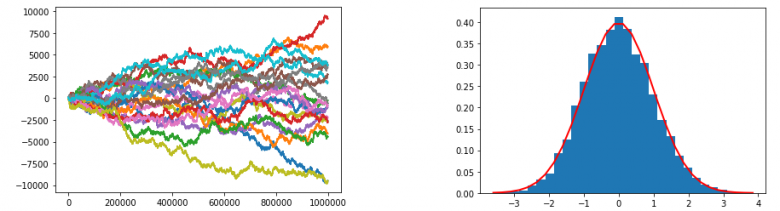
Paramètres convergence en loi vers une loi normale

Posté par
Kernelpanicre : Paramètres convergence en loi vers une loi normale 21-05-20 à 10:40

Bonjour WilliamM007, merci beaucoup de ta réponse !

Donc sans trop de surprise : il y a bien une coquille, le racine de n a sauté. Mon professeur de TD qui nous a envoyé le sujet étant nouveau cette année, il n'a pas fait attention et n'a pas été prévenu de la coquille.

Pour cette astuce, c'est lié à la fonction génératrice non ? Plus généralement, si X suit une loi de Poisson de paramètre \lambda, on a :

\mathbb{E}[X(X-1)...(X-k+1)] = \lambda^k

? (sauf si j'ai fait une erreur de calcul ou de récurrence)

Et merci pour ce superbe histogramme, je peux te demander comment tu l'as réalisé ? Si c'est sur Excel ou avec un autre langage

Posté par
lionel52re : Paramètres convergence en loi vers une loi normale 21-05-20 à 10:57

Ah ca c'est du matplolib sur python!

Posté par
WilliamM007re : Paramètres convergence en loi vers une loi normale 21-05-20 à 10:58

Citation :
Pour cette astuce, c'est lié à la fonction génératrice non ? Plus généralement, si X suit une loi de Poisson de paramètre \lambda, on a :

\mathbb{E}[X(X-1)...(X-k+1)] = \lambda^k

? (sauf si j'ai fait une erreur de calcul ou de récurrence)

Pour moi pas besoin de fonction génératrice ou de récurrence. C'est direct (c'est un peu l'intérêt de prendre ce polynôme et non pas directement X^k) :

\mathbb{E}[X(X-1)...(X-k+1)]=\sum_{n=0}^{+\infty}n(n-1)\cdots(n-k+1)\textrm e^{-\lambda}\frac{\lambda^n}{n!}=\textrm e^{-\lambda}\lambda^k\sum_{n=k}^{+\infty}\frac{\lambda^{n-k}}{(n-k)!}=\textrm e^{-\lambda}\lambda^k\textrm e^\lambda=\lambda^k.

Citation :
Et merci pour ce superbe histogramme, je peux te demander comment tu l'as réalisé ? Si c'est sur Excel ou avec un autre langage

En Python, tout simplement. Voici le code si ça t'intéresse (oui il est horriblement écrit je sais) :

import numpy as np
import matplotlib.pyplot as plt

n = 100
p = 1000 # nombre de simulations

x = np.zeros((p,n))
y = np.zeros((p,n))
for k in range(p):
    x[k] = np.cumsum(np.random.poisson(1, n)**2)-2*np.arange(1, n+1)
    y[k] = x[k]/np.sqrt(11*np.arange(1,n+1))
x = x.transpose()
y = y.transpose()
plt.plot(x)
plt.show()
plt.close()

count, bins, ignored = plt.hist(y[n-1], 30, density=True)
plt.plot(bins, 1/(np.sqrt(2 * np.pi)) * np.exp( - (bins - 0)**2 / (2 * 1**2) ), linewidth=2, color='r')
plt.show()

Posté par
WilliamM007re : Paramètres convergence en loi vers une loi normale 21-05-20 à 10:59

lionel52 @ 21-05-2020 à 10:57

Ah ca c'est du matplolib sur python!

on a un connaisseur

Posté par
Kernelpanicre : Paramètres convergence en loi vers une loi normale 21-05-20 à 11:18

Merci beaucoup (encore une fois) ! Va falloir que je me remette à Python, j'ai tout oublié à cause du C, C++ et Java lorsque je faisais anciennement ma double licence informatique...

Bonne journée


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1674 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !