Inscription / Connexion Nouveau Sujet
Parasites triangulaires
Bonjour à tous 
Un petit peu d'humour pour changer un peu des tirages de boules 
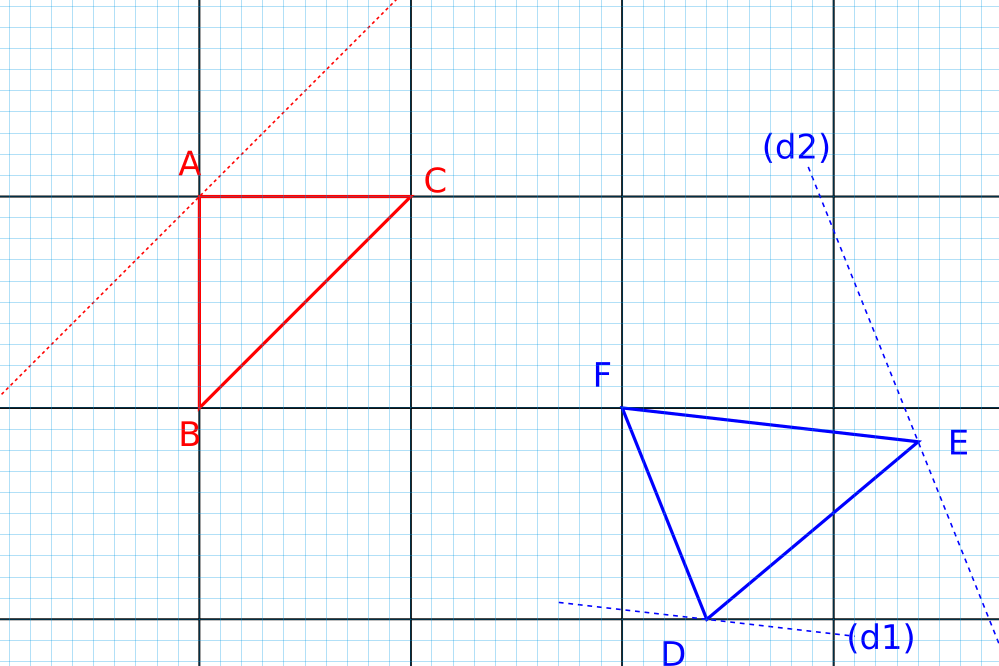
Les stablaires à membrane élastique sont des parasites à reproduction sexuée . Ils sont de forme triangulaire et se déplacent sur un plan de façon étrange . Ils restent triangulaires en conservant leurs aires sans que deux de leurs sommets puissent bouger en même temps . Les SME ont des formes diverses et ils ne peuvent malheureusement se reproduire qu'avec des partenaires de même aire . Les opportunités sont donc plutôt rares et sans rentrer dans les détails de l'acte , pour que l'accouplement se produise il faut que les deux partenaires occupent exactement la même place .

La rencontre entre deux SME compatibles ( et consentants ) est-elle toujours possible ?
Imod
Bonjour,
Quelques conjectures :
* La règle de déplacement n'autorise que le déplacement d'un sommet parallèlement à sa base.
* Un SME T0, de sommets A0B0C0 peut toujours devenir un triangle rectangle isocèle en A0 quitte à renommer les sommets (le triangle se sera bien sûr déplacé durant cette transformation). Déformons ce SME et appelons-le toujours T0. Car alors tout triangle compatible avec ce nouveau T0 sera compatible avec l'ancien.
On construit un carré en ajoutant le symétrique de A0 par rapport à B0C0. Puis on copie-colle ce carré pour former un quadrillage remplissant tout le plan.
* Alors il semblerait que tout triangle de même aire et ayant 2 sommets sur ce quadrillage peut se reproduire avec T0.
Pas mieux pour le moment ... Il y en a certainement d'autres.
Bonjour à tous les deux 
@Thetapinch27 : je n'ai pas encore tout regardé car je bloque dès le départ , je ne vois pas comment tu passes d'un triangle quelconque à un triangle rectangle-isocèle . Sinon le déplacement parallèle est bien sûr la bonne idée .
Imod
Bonsoir,
je ne vois pas comment tu passes d'un triangle quelconque à un triangle rectangle-isocèle .
Imod
Voici le procédé.
Soit un triangle quelconque d'aire 1/2.
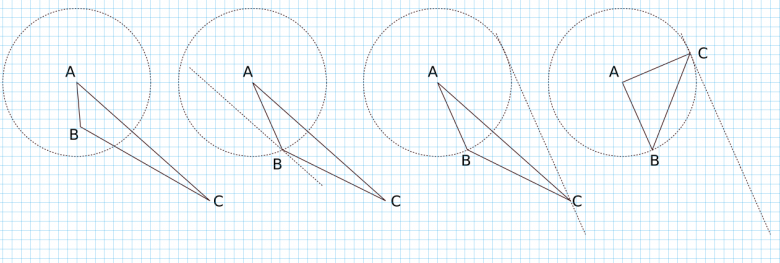
* On trace un cercle de rayon 1 autour d'un sommet touchant le plus petit des trois côtés.
* Déplacer B (le plus proche de A) jusqu'au cercle.
* Puis on déplace C parallèlement à (AB), sur une trajectoire qui tangente nécessairement le cercle, et jusqu'au point de tangence. Ce point existe nécessairement car C doit couper la perpendiculaire à (AB) passant par A vu qu'il se déplace parallèlement à (AB), et qu'alors en ce point l'angle BAC=90° et donc AC=1 (car aire = 1/2).
Après je pense que ce passage par les triangles isocèles n'est pas nécessaire pour le raisonnement mais il m'a bien aidé à fixer les idées. Car on pourrait probablement faire un maillage de parallélogrammes avec le triangle initial sans chercher à le transformer en isocèle rectangle, et positionner le second triangle sur les points de cette grille "non-orthonormée".
Bonne soirée
Tu as trouvé le mécanisme pour déplacer les sommets et en effet les triangles isocèles ou rectangles ne servent pas à grand-chose ni même le quadrillage mais ça peut encadrer la recherche . Plus simplement , si on note ABC et DEF les deux triangles , quitte à renommer au besoin les sommets de DEF , on peut amener A en D en deux mouvements puis de même B en E et pour finir C en F . Par exemple pour A , on déplace C parallèlement à (AB) , la droite (BC) va alors prendre toutes les directions possibles sauf celle de (AB) , on choisit donc (BC) // ((AD) et on amène A en D . On amène de même B en E . La stratégie change un peu pour le troisième point .
Imod


 Cliquez pour afficher
Cliquez pour afficher