Bonjour,

Pour répondre ,il nous faudrait la partie concernée de l'énoncé.

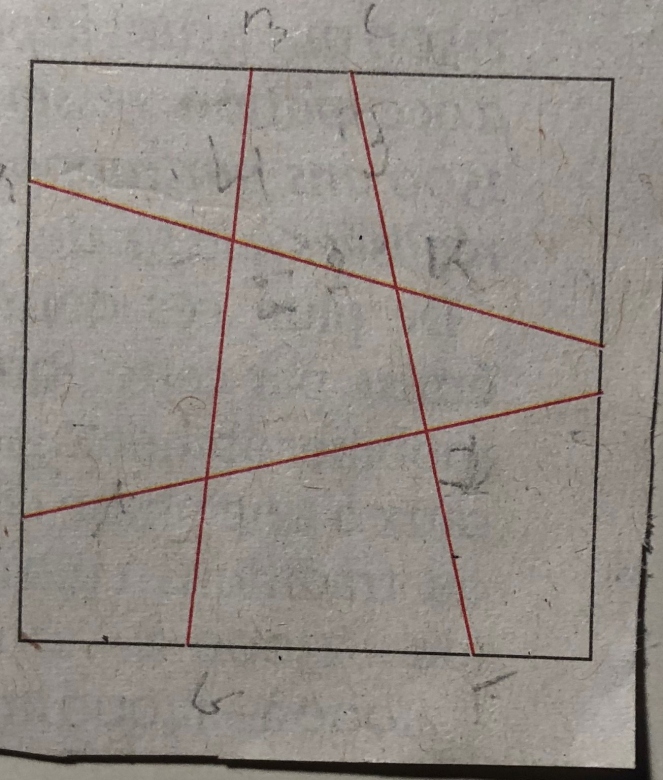
On découpe un carré  selon 4 segments(en rouge)afin d'obtenir 9 quadrilatères dont les aires en dm carré forment un carré magique 3x3: la somme des 3 aires de chaque rangée, de chaque colonne, et de chaque diagonale principale est toujours la même.
1) Chaque segment rouge passe par un point précis . Lequel ?
2) les aires des 9 quadrilatères, exprimées en dm carrés, sont des entiers consécutifs.
Est ce possible avec les entiers 1 à 9 ? avec les entiers 2 à 10 ?
3)(difficile) Avec les entiers 3 à 11 ?

Merci,

On voit de suite que construire le quadrilatère le plus petit est difficile...
Je chercherai  dans la journée.
Je connais des îliens qui vont aimer...

Bonjour

Le site Diophante avait proposé une version de ce problème il y a quelques mois . Il y a une construction quasi géométrique des solutions quand elles existent .

Un indice :

 Cliquez pour afficher

Observer les milieux des segments rouges .

Bonjour

 Cliquez pour afficher

Excuse je ne voulais pas donner l'image mais le "blanke" n'a pas fonctionné

Bonjour,
J'ai rectifié

Suite

Je réponds à la question1.

 Cliquez pour afficher

En fonction des carrés magiques on a un carré de dimension:

1 à 9  total  45 coté  456.71
2 à 10 total  54 coté 54 7.35
3 à 11 total  63 coté 63  7.94
le milieu des obliques  forme un  carré de  diagonale  c/3 et donc de coté  (c2)/6

soit

 Cliquez pour afficher

suite,

 Cliquez pour afficher

On observe que l'aire du quadrilatère du milieu est égale au double de l'aire
du carré formé par les ponts centraux des obliques  ça devait servir...

Suite,
Il semble difficile de tracer le polygone central qui sera le générateur
de l'ensemble.
Je donne l'ensemble de ses caractéristiques .
1) soit l' option  3 à  11  total 63
2)coté du grand carré C=63 =37  
3)diagonale du petit carré c =C/3=7
4)coté c =c/2
5)aire du carré central   =(7/2)²=3.5
6)aire du quadrilatère central =7 par définition à construire autour du carré inscrit c
7)l'aire des 4 triangles  =3.5
soit somme des hauteurs  = 2c
Je donne une valeur approchée  h1=1.5  h2=0.65  h3 =0.6  h4=0.99
avec =67° =95° 112 ° 86°.

C'est donc possible il reste à trouver les valeurs exactes

Bonjour, il semble que ce sujet (pb 1156 du monde)a déjà reçu  une solution, et même qu'li y ait  une construction géométrique. Ou peut-on les trouver ?
Merci de votre attention

Je pense que la solution réside dans la construction du quadrilatère ABCD
connaissant son aire double de celle du carré gris inscrit  de coté  c connu MNOP.

Pour 2 à 10   c=3.

Tout dépend de ce que l'on appelle construction géométrique . Des logiciels comme Geogebra intègrent tellement de fonctionnalités que tout devient géométrique .

Voilà comment j'ai vu les choses :

Je ne blanke plus car je n'en vois pas l'intérêt .

On part du carré magique démarrant à 2 :



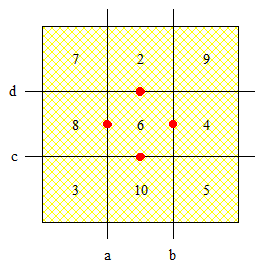
Les valeurs dans les carrés sont les aires attendues et les droites a , b , c et d pivotent autour des points rouges en évitant les croisements . Au départ toutes les aires sont égales à 6 et on note les cases comme celles d'un échiquier .

Une première remarque : si les aires des cases A1 , A2 , B1 et B2 sont celles indiquées sur le dessin alors les autres le sont aussi . Prenons maintenant la position de la baguette b comme variable . On va alors dans l'ordre :

1°) Positionner c pour que A1 + B1 = 13 .

2°) Positionner a pour que A1 = 3 .

3°) Positionner d pour que A2 = 8 .

On peut alors calculer B2 ( c'est à dire l'exprimer en fonction de b ) .

Il n'y a plus qu'à voir si 6 est dans l'intervalle des valeurs prises par B2 sous les contraintes annoncées .

Imod

>pisurdeux
Comme le dit Imod, cet exercice a été proposé sur Diophante par Michel Lafond.
Il existe  une dizaine de démonstrations assez élégantes.
Chercher : Diophante carré magique  B 138

Merci à tous, en particulier à lmod, pour leur contribution.
J'ai grâce à vous la réponse à ma question initiale : y a t-il une solution pour les aires 2 à 10? (réponse oui).
On peut clore ce sujet.

Bonjour,
"Diophante carré magique B 138" donne une solution pour les entiers de 5 à 13, pas pour les entiers de 2 à 10.

Et attention , il faut bien sûr vérifier que 6 est une valeur possible pour B2 quand on on fait tourner b mais aussi qu'il n'y a pas de croisement entre les baguettes à l'intérieur du carré car cela fausserait tout .

Imod  

Bonjour, à l'attention de sylvieg : Exact, mais on peut appliquer une des méthodes de Diophante B138 au cas des nombres 2 à10  et  à n'importe quel cas n à n+8, sauf n=1, pour trouver une solution (deux solutions si n>2).

J'ai été voir la solution donnée au problème du Monde dans le site "affaire de logique" :
Il faut être inscrit pour y avoir accès.

Je m'appuie sur la figure de Imod pour résumer ce que j'y ai compris pour les aires 2 à 10.
Remarquer ceci d'abord :
On veut entre autres :
Aire B3 = 2 , aire B3 + aire B2 = 8 = 4aire B3 et aire B3 + aire B2 + aire B1 = 18 = 9aire B3 .

Le domaine B3 (en haut au milieu) doit avoir une aire égale à 2.
C'est le cas si les baguettes a et b se rejoignent sur le côté supérieur du carré et que la baguette d est horizontale. Le domaine a alors la forme d'un triangle.
Si on écarte les baguettes a et b, alors l'aire du domaine B3 augmente.
Idem si on fait pivoter la baguette d.
Il est donc démontré que les baguettes a et b doivent se rejoindre sur le côté supérieur du carré et que la baguette d doit être horizontale.

Avec ces conditions remplies, la réunion des domaines B3 et B2 doit avoir une aire égale à 8.
Ce qui est réalisé quand la baguette c est aussi horizontale.
Si on fait pivoter la baguette c autour de son milieu alors l'aire augmente.
Il est donc démontré que la baguette c doit aussi être horizontale.

La contradiction viendrait alors de la non monotonie des aires A1, A2 et A3 ?

@pisurdeux,
Où penses-tu avoir trouvé une erreur ?

>derny
Mes approximations donnent à peu près ton dessin.
Comment as-tu procédé?  Merci

Bonjour
dpi, en fait je n'ai rien calculé faute de temps. Pourtant ce sujet m'intéresse. J'ai simplement "pompé" un croquis donné.

J'aimerais bien un dessin avec 2,3,4,5,6,7,8,9,10.
Même s'il n'est qu'approché.
Puisque pisurdeux affirme qu'il y a une solution

Bonsoir
sylvieg, voilà ce que j'ai pompé.

Mes approximations concernaient le quadri central de  3 à  11 (7)

Je vais essayer de définir celui de 1 à  10 soit 6

Je pense ,hélas! que la figure 2 à 10 n'est pas faisable:
Je reste sur mon modèle du 7/10 15h02:

cas 2 à 10-->somme 54-->C=36-->c=3-->aire=3
Il faut donc trouver un quadrilatère inscrivant ce carré et ayant une aire égale à 6-3=3.
On sait bien sûr que le carré de rotation/4 convient .
Les 4 triangles formant le complément auront des hauteurs dont la somme sera 3.
Analysons la figure "pompée" de derny .
On arrondi =60°  =85° =115 °et =100 °.
Dans les triangles ,en divisant leur angle et leur base par 2 ,avec la tangente on obtient
la hauteur.
Par exemple h1= 1.5 .La somme  s des hauteurs trouvées est  3.72 >3
Quels que soient les angles du quadrilatères on obtiendra toujours s>3 (sauf le carré)

Merci derny pour le "pompage".
Merci aussi à dpi pour le commentaire.
Pas trop le temps ce matin.
Mais je remarque déjà que les baguettes qui délimitent l'aire 2 se coupent bien sur le côté du carré.
Après, pour la 3ème baguette qui délimite 2, à voir si elle doit obligatoirement être parallèle au côté du carré, comme affirmé dans la solution du site "affaire de logique".

correction......

La somme des hauteurs doit être  2c donc  23
3.46

Bonjour
dpi es tu sûr de 3.72 comme somme des hauteurs. Il me semble que c'est moins en mesurant simplement sur un croquis approximatif il est vrai ?

Sans préjuger de la faisabilité d'une figure pour 2 à 10, je pense que le raisonnement donné dans affaire de logique est faux.

L'erreur est dans la seconde ligne de cet extrait de mon message du 9 à 18h15 :

>derny
Heureusement que mathafou n'a pas vu ma magnifique
démonstration qui obtient la hauteur d'un triangle avec
seulement  sa base et son angle au sommet
Donc tu as raison ,reste à trouver les véritables angles de cette maudite
figure.

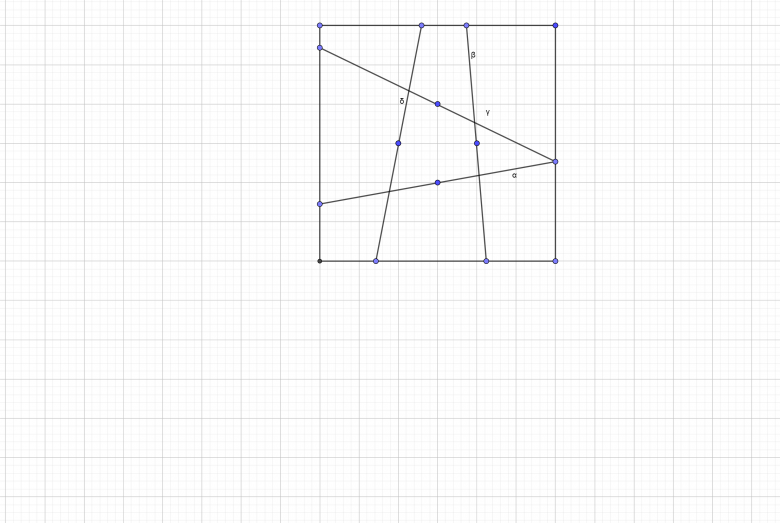
Je réaffirme qu'il y a une solution pour les aires 2 à 10, voici un  dessin : les angles α et γ sont avec l'horizontale, β et δ avec la verticale (peut on tracer des lignes pointillées dans Géobra?); tan( α)=0,265901; tan(β)=0,093682; tan(γ)=-0,399002; tan(δ)=-0,257258.
L'erreur dans la solution du Monde a été de supposer, sans justification, que l'aire minimale d'un quadrilatère  est obtenue s'il est réduit à un triangle et limité par une verticale (aire minimum 1/27 du carré). Si on limite le triangle par une droite de pente 3/2, l'aire minimum passe à 4/135 du carré, soit 4/135*54=8/5 pour les aires 2 à 10.

Oui, pisurdeux,
L'erreur est dans le "limité par une verticale".
C'est ce que j'explique aussi dans mon message de ce midi

Je n'ai pas regarder les derniers développements , mais il me semble que dans l'énoncé on demande 9 quadrilatères . Dès que la construction du "2" exige un triangle , il n'y a plus de solution , non ?

Imod

Effectivement, c'est un argument ; mais ce n'est pas celui utilisé dans le site "affaire de logique"

>pisurdeux
Bravo!
On ne voyait pas trop où étaient situés tes angles.
Il ne reste plus qu'à donner les points de la bonne figure
avec tes tangentes..

@pisurdeux,
Avez-vous signalé l'erreur au site "affaire de logique" ?

Je ne suis pas inscrit sur le site "Affaire de logique" , la solution décrite par Sylvieg est-elle celle qui a été ( sera ?) proposée aux lecteurs du "Monde" ?

Imod

Voici  enfin la solution 2à 10 .

Il faudrait légèrement changer  les ultimes décimales des tangentes de

 Cliquez pour afficher

pisurdeux

Je me suis inspirée de la solution proposée sur le site "affaire de logique" pour la question 2.
Pour la question 3 le site précise qu'elle "était trop longue pour tenir dans la rubrique "papier" du Monde daté du 16 septembre."

C'est moi qui aie ajouté l'histoire des aires multipliées par 2² et 3².
J'y voyais du Thalès avec les parallèles.
Mais finalement ça tombe à l'eau.

Observation:
En faisant la vérification de la somme  des cotes de mon dessin il  semblerait que le
"triangle" 2 soit en fait  lui aussi un quadrilatère avec un minuscule coté de 0.0065
coté gauche.

Bonjour.
@lmod : Les 9 quadrilatères pour les aires 2 à 10 sont des vrais quadrilatères. Le quadrilatére 2 a un coté vertical de longueur 0,0098, ce qu'un dessin ne peut pas montrer.
@silvieg : j'ai signalé l'erreur au site des éditions pole, sans réponse. Ce n'est pas la première fois que cela se produit.
@dip : les 6 décimales des tangentes (ou des pentes des droites) sont, à mon  avis, exactes.
Mon logiciel (en C, long double de 80 bits) affiche les aires des 9 quadrilatères, elles ont au moins 12 chiffres significatifs exacts.

Observation:
J'ai été tenace........
En faisant la vérification de la somme  des cotes de mon dessin il  semblerait que le
"triangle" 2 soit en fait  lui aussi un quadrilatère avec un minuscule coté de 0.0065
coté droit.
Donc les tangente de pisurdeux  sont valables ;il suffit de rectifier le dessin

Vous faites trop confiance à vos logiciels de dessin

On peut démontrer par calcul que la part "2" est bien un triangle .

Imod

>Imod

Ce n'est pas avec un logiciel de dessin mais c'est mon péché sur Excel.
C'est curieux mais le dessin de  pisurdeux m'a inspiré et encore plus ses tangentes.
En remontant on arrive bon pour le haut et le bas,mais à gauche et à droite il
manque 0.0065 qui ne peuvent correspondre qu'au minuscule coté du quadrilatére
"triangulaire".
Je t'encourage à faire les calculs sur mon dessin de 14h52

Bonjour,
@Imod,
La part "2" peut ne pas être un triangle.

Si le point U est confondu avec le point P, l'aire du triangle PXY est égale à 2.
Celle du triangle PWV est donc inférieure à 2 puisque l'aire du triangle LXW est supérieure à celle du triangle LYV.
La condition P et U confondus tombe aussi à l'eau puisqu'on peut donc écarter le point U du point P pour obtenir un trapèze PUVW d'aire 2.

@pisurdeux,
J'ai envoyé un courriel aux éditions Pole, à l'attention des trois auteurs du site "affaire de logique", avec les arguments et la figure ci-dessus.

Petit correctif
La part "2" est peut-être un triangle dans la solution de 2 à 10.
J'affirme seulement ceci :
Si on n'impose rien aux autres aires, on peut obtenir un vrai trapèze d'aire 2 dans un carré d'aire 54.

>Sylvieg
Je suis sûr de mon dessin du12/10 à 14 h52.
Le petit coté du faux triangle mais du vrai quadrilatère mesure 0.0065
En vérifiant toutes les zones on t exactement une aire égale à 18

J'ai essayé de voir "à la main" s'il y avait 0, 1 ou 2 solution(s) et j'ai ma réponse même si un esclave est indispensable pour conclure

Je commence par ramener le côté du carré à 6 pour ne pas traîner des expressions infernales :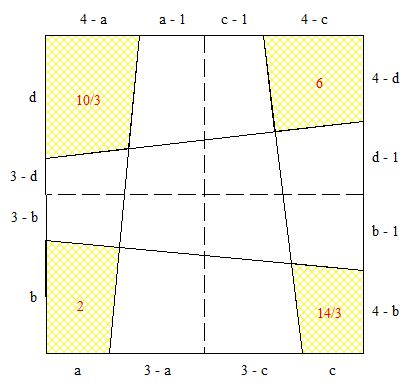



On peut donner les coordonnées du quatrième sommet des quadrilatères jaunes à l'aide de a , b , c et d et exprimer leurs aires à l'aide des mêmes paramètres . On aboutit à quatre équations à quatre inconnues que je n'ai pas le courage de recopier . On met tout ça dans la machine et on obtient deux solutions que j'ai ramenées aux dimensions initiales :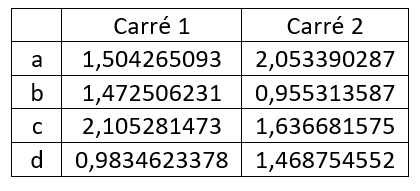



La première solution est celle qui a été proposée ici et la deuxième n'est pas valide car .

Le problème a donc une solution unique .

Imod