Inscription / Connexion Nouveau Sujet
Pb de géométrie
Bonjour,
Je travail sur la réalisation d'un robot autonome, plus particulièrement sur la programmation d'un télémètre laser à balayage. Ce télémètre a pour objectif de calculer des distances entre mon robot et un obstacle afin d'effectuer une procédure d'évitement.
En effet, le capteur sera orienté à un angle de 45° lorsqu'un robot adverse se trouvera à une distance assez proche. Cela nécessite alors de faire une projection car les valeurs reçues ne seront pas traitable directement afin de déterminer la position XY exacte de l'obstacle par rapport à mon robot. Je cherche donc à exprimer la distance AB en fonction de CB et de l'angle α (voir la modélisation 3D). Pour l'instant je n'ai trouvé la solution que dans le cas particulier où le scanner fait un tir tout droit.
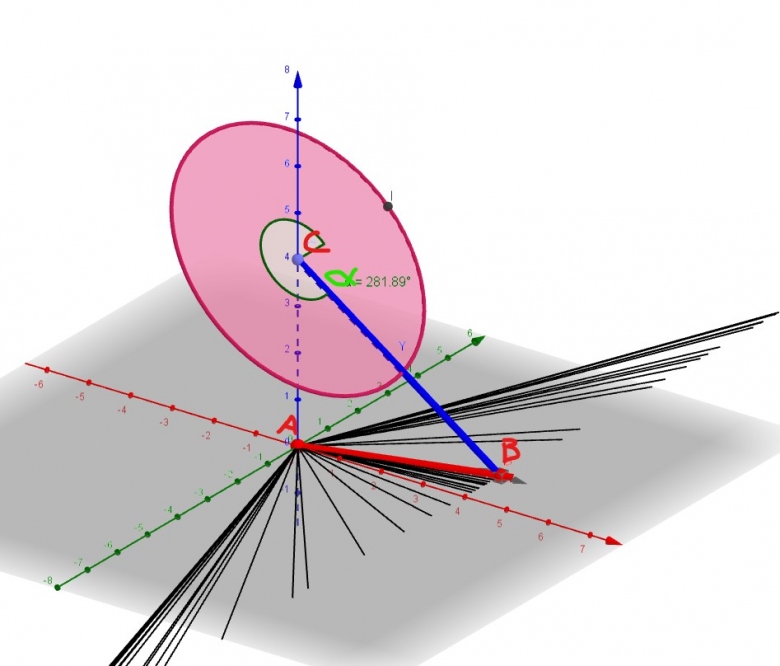
Si représente l'angle de l'arc de cercle vert et si le point i délimite ton arc de cercle vert alors comme tu connais
=281,89° tu doit connaître l'angle délimité par l'axe bleu et le point i notons cette angle
.
Ainsi l'angle ACB=-180°-
Comme
Alors
Il faut préciser les données de ta modélisation 3D.
Bonjour,
Ta description manque de précision/clarté.
La façon dont je l'interprète :
Je note la base orthonormée de l'espace qui correspond aux axes rouge, vert bleu de ton schéma (du Geogebra 3D, visiblement).
Ton disque rose est, si je comprends bien, orthogonal au vecteur . Ton point
a l'air d'être tel que le vecteur
a même direction et même sens que
. Confirmes-tu ? Le vecteur unitaire qui a même direction et même sens que
est alors
.
Le produit scalaire avec te donne donc le cosinus de l'angle géométrique entre
et
.
Je te laisse cogiter à partir de ça pour avoir l'expression de en fonction de
et
.


 géométrie en post-bac
géométrie en post-bac