Bonsoir et bonne année.

 Cliquez pour afficher

Une solution en pesant 112 pièces :
sac1 :  0 pièce
sac2 : 1 pièce
sac3 : 3 pièces
sac4 : 4 pièces
sac5 : 12 pièces
sac6 : 13 pièces
sac7 : 39 pièces
sac8 : 40 pièces
on 1120g du résultat puis on lit le résultat dans le tableau

La masse totale des 56 pesées possibles est 65 072g.

Bonsoir verdurin, bonne année a toi aussi.

Désolé mais  ce n'est pas la bonne réponse.

Pour compléter ma réponse, le sujet indique qu'il faut prélever un minimum de pièces dans les sacs en partant d'un nombre maximum de 100piéces (alors que tu pars d'un minimum de 0 pièces et ajoutes des pièces)

Je crois volontiers que ma solution n'est pas optimale ( je n'ai pas cherché longtemps ) mais le minimum de pièces que l'on peut prendre dans un sac est bien 0.
Et toutes les valeurs que je donne sont bien inférieures à 100.

Je ne comprends pas ton dernier message.

Une remarque au passage : il m'aurait semblé préférable que les fausses pièces aient une masse inférieure aux vraies. Mais c'est un détail sans réelle importance.

Bonjour,
L'idée de verdurin est intéressante ...

 Cliquez pour afficher

en prenant une pièce du sac 1,deux pièces du sac2----huit pièces du sac 8 on obtient un total de 3600 g+x

x étant  11a +12b
on fait une grille  des possibles :
Par exemple si P=3693 g x=93 et les pièces fausses de 11 g sont dans le sac 3 et celles de 12g dans le sac 5.
A noter que tous les totaux sont différents.

Un petit décalage  vers la fin..

 Cliquez pour afficher

et tableau complémentaire.

Bonjour,

 Cliquez pour afficher

Les nombres de pièces à retirer des différents paquets sont :

0, 1, 3, 8, 21, 24, 52, 55

La somme des 56 masses différentes possibles est  :

164*10 + 3444 = 5084 g

@verdurin,

Bonjour,

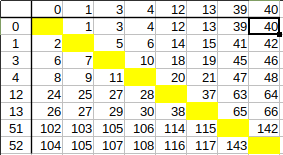
Il me semble que dans ton tableau les nombres de la ligne du haut devraient être les mêmes que ceux se la 1ère colonne... et ce n'est pas le cas pour les 2 derniers.

De toutes façons ma solution était fausse car 41+12=01+32.
Il y a donc deux configurations différentes qui donnent la même masse.

Une solution correcte mais sans doute pas optimale.

 Cliquez pour afficher

Je continue un peu plus tard car le temps de chargement de l'image précédente m'a effrayé.

À dpi, les masses que tu obtiens ne sont pas toutes différentes.
Par exemple 2 pièces de 12g, 1 pièce de 11g et 33 pièces de 10g pèsent 355g comme 3 pièces de 11g,  1 pièce de 12g et 32 pièces de 10g.

À candide2 il manque une multiplication par 56 dans ton calcul de la masse totale des 56 possibilités. Je trouve 95 284g.

Sinon j'ai trouvé une solution meilleure que celles données plus haut. Avec une masse totale de 80 178g.

bonsoir , une idée :

 Cliquez pour afficher

On numérote les sacs de 1 à 8.
On prélève 1 pièce du sac 1, 2 pièces du sac 2, …, 8 pièces du sac 8, soit au total 36 pièces.

Si toutes les pièces étaient vraies (10 g chacune), la masse totale serait de
36 × 10 = 360 g.

Dans le cas réel, on pèse l'ensemble des pièces prélevées et on obtient une masse M.
La quantité M − 360 représente alors l'excédent de masse dû aux fausses pièces, puisqu'il y a exactement deux sacs contenant des pièces plus lourdes.

Si x est le nombre de pièces prélevées dans le sac contenant des pièces de 11 g et y le nombre de pièces prélevées dans le sac contenant des pièces de 12 g, alors l'excédent vérifie l'équation diophantienne : x + 2y = M − 360.  

On est donc ramené à la résolution d'une équation diophantienne, où x et y doivent appartenir à l'ensemble {1,2,…,8} et correspondre aux quantités prélevées dans deux sacs distincts.

En connaissant la valeur mesurée M, on peut déterminer les couples (x, y) compatibles et en déduire les sacs susceptibles de contenir les pièces de 11 g et de 12 g.

Cette méthode repose sur une seule pesée et un prélèvement minimal, tout en mettant en évidence la condition d'unicité nécessaire pour identifier sans ambiguïté les deux sacs.....(ce n'est pas peut être pas la façon de faire attendue .....)

Bonsoir flight,
comme  je l'ai fait remarquer à dpi dans le message précédent ça ne marche pas.

Bonjour Flight,

Dans ce problème, ta tactique ne fonctionne pas.

Par exemple si on détecte par la balance un écart de masse de 9 g, on ne peut trancher entre les 2 options ci-dessous :

1°) 7 pièces de 11g du sac 7 et 1 pièce de 12 g du sac 1
2°) 5 pièces de 11 g du sac 5 et 2 pièces de 12 g du sac 2

Il y a beaucoup de delta masse possibles qui proviennent de plusieurs combinaisons de sacs.

Curieusement dans mon tableau on constate que les 56 sommes
sont différentes si on rectifie 5x12+6x11 =126 non 132  ce qui un certain temps m'a fait pensé à une solution valable .
Il y a certainement une exploitation utile de ce constat.

Je savais bien que mon idée était exploitable:
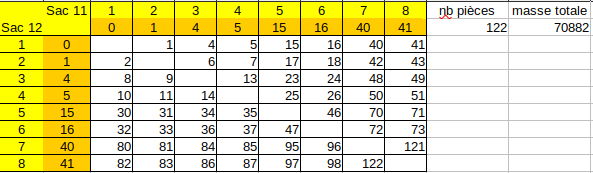
* on numérote les sacs de 1 à 8
*on prend 8 pièces dans le sac 1 ;16 dans le sac 2-----80  pièces dans le sac8
Si  toutes les pièces étaient vraies on pèserait  2880 g
Les pesées suivantes donnent dans quels sacs sont les fausses de 11 g et celles de 12g

Damned
erreur dans les totaux

Bonjour,

Pas la seule erreur dpi, ta phrase :

"*on prend 8 pièces dans le sac 1 ;16 dans le sac 2-----80  pièces dans le sac8 ", ne permet pas de connaître le nombre de pièces à prélever dans chacun des sacs.
Le "80" est hors des clous, je comprendrais si c'était "64" à la place de 80 ... Bien que cela ne convient pas.

Ok! j'attends la solution idéale

Il y a une répartition des billes à enlever dans le message du  06-01-26 à 11:12 qui permet de déterminer en une pesée les 2 sacs à pièces différentes... mais cette répartition n'est pas celle qui permet de prélever le minimum de pièces des sacs.

Dans le message du 06-01-26 à 16:12, verdurin a donné une autre  répartition des billes à enlever ... et cette répartition prélève moins de pièces que la mienne, donc elle est plus proche de ce qui demandé... Mais comment déterminer si cette répartition est la meilleure ?  ...  je ne sais pas.

En fait je ne vois guère d'autres méthodes que des tests exhaustifs par programme pour être certain d'avoir la configuration optimale.

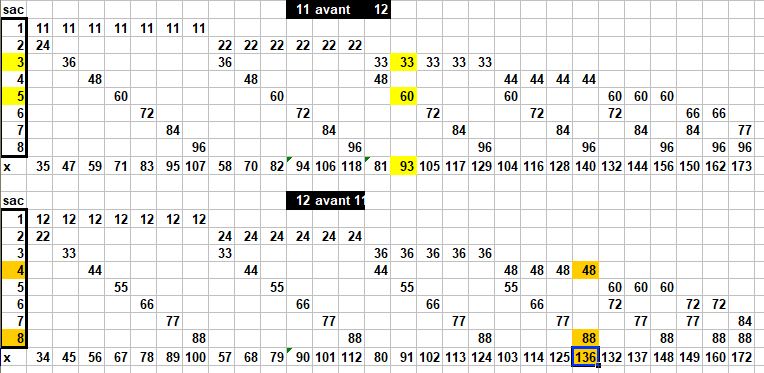
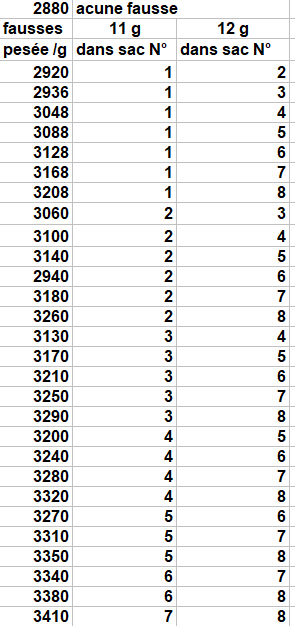
Voici la meilleure répartition que j'ai trouvée, je pense qu'elle est optimale sans en être complètement certain.

 Cliquez pour afficher

le nombre de pièces prélevées est dans la zone orange. Il faut rajouter 1220g aux résultats dans le tableau pour avoir la masse indiquée par la balance.

Je me suis basé sur le fait que le prélèvement (a, a+1) permet de distinguer deux sacs et que le prélèvement  (a-1, a, a+1) introduit toujours une confusion.
À partir de là j'ai fait de l'optimisation locale.

Bonjour,
>verdurin  et

Dois-je comprendre que si la pesée donne  1267 g ,cela signifie que
les fausses  pièces  de 11 g sont dans le sac 5 et celles de 12 g dans le
sac 6 ?

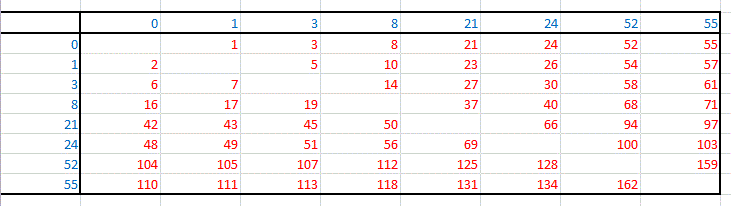
Je propose 0,  1, 4, 5, 16, 17, 19, 21.
On remarque le motif 0,1 répété avec un décalage de 4 pour donner 0,1 4,5 lui-même répété avec un décalage de 16.

16, 17  20, 21 pardon

Soit
On pourra remarquer que est l'ensemble des entiers naturels .
Et vous pouvez deviner sans peine comment on ferait avec 16 sacs. Que serait ?

Pour ce qui est de la somme des 56 masses :
On a à chaque fois 84 pièces ce qui ferait 56 x 840 g.
Mais il y a les excès dus aux fausses pièces. La somme de ces 56 excès  en grammes est la somme des entiers de 0 à 63 moins la somme des triples d'éléments de , soit 3 x 84.
Au total, 48 kilogrammes 804 grammes.

Bravo.
Là on est sur d'avoir le minimum.

Bravo GBZM c'est la bonne réponse !

J'avais une panne de courant depuis 18 h...
Entièrement d'accord .
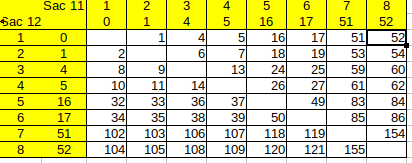
J'avais fait le tableau façon verdurin  avec le données GBMZ
A noter que  les cas d'un seul sac faux sont à exclure.

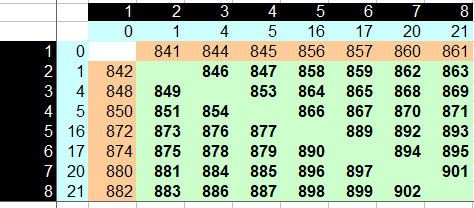
Il est plus parlant de faire figurer les excès au-dessus de 840, et de compléter le tableau avec sa diagonale. On voit alors apparaître tous les entiers de 0 à 63, une fois et une seule.

Comme il s'agit de  répondre en une seule pesée , on obtiendra de 844 à 902 g et en fonction du tableau on pourra affirmer 11 dans le sac N° A et 12 dans le sac N° B.
Par exemple  867 g = pièces de 11 g dans sac N° 6  celles de 12 g dans sac N° 4
à  noter qu'on  n'aura jamais  841 ,842,843,848,850,852 ,855,856, 872, 874 ,880 ,882,891,895

* les pesées en rouge ne sont pas dans le tableau
*les autres ne donnent qu'un seul sac alors qu'il y en a forcément 2

Tu te trompes, dpi.
Par exemple, on peut obtenir 841g., dans le cas où les pièces à 12g sont dans le sac 1 et selles à 11g dans le sac 2.

C'est vrai que  2x0+1x1  =1
Donc ne retenir que les nombres en rouge.