c'est dure à expliquer

10 ans après

même si ça ne sert plus à rien

Je pense qu'il y a prescription .

que signifie d'ailleurs la question ? ....

Bonjour,

pas grand chose à mon avis ... d'où l'absence totale de réponse à l'époque (en plus de la raison d'absence de forme de politesse)
on ne "démontre" pas un nombre
on le calcule, on démontre qu'il a telle et telle propriétés etc ...

Ce certain Hobson dont on parle dans la biographie de Ramanujan ne semble pas avoir laissé de méthode immortalisée concernant en quoi que ce soit pi en plus. à moins de trouver ça dans un obscur écrit du dit sieur Hobson, qu'on pourrait se procurer à prix d'or chez un bouquiniste ou sur JStor ...

Il n'y a pas à chercher beaucoup :

J'étais donc mauvaise langue, mais mes recherches avaient été complètement infructueuses via Gogole, à part la référence à Ramanujan et tout un tas de centaines de Hobson sans rapport avec celui là.

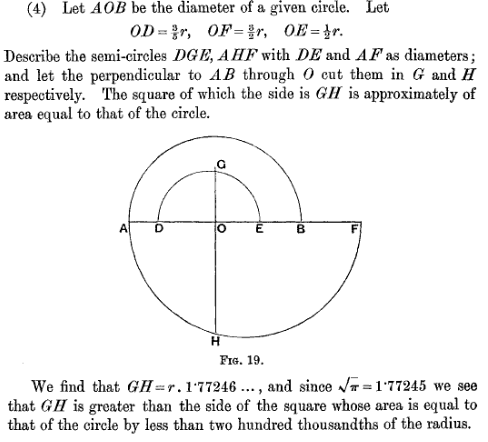
La quadrature approchée décrite ci-dessus donne comme valeur pour le côté du carré fois le rayon, qui excède de ("less than two hundred thousands").

two hundred thousandths, excusez-moi.