Inscription / Connexion Nouveau Sujet
Pliage d'un disque
Bonjour,
issu d'un problème de concours :
Étant donné un disque de papier, et deux points A et B de son pourtour,
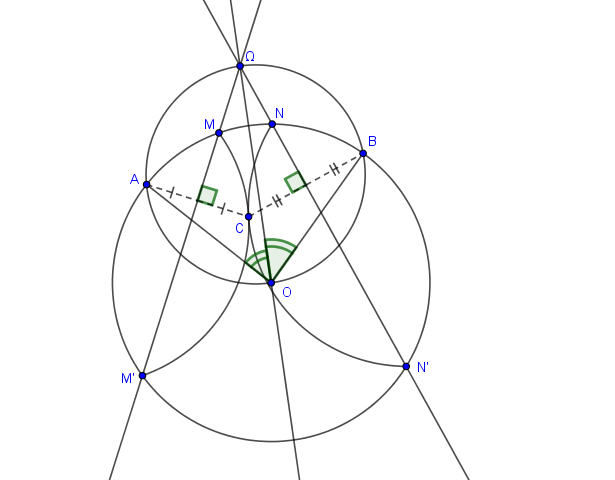
on cherche à le plier de sorte que les points A et B viennent en C, point de tangence des deux parties pliées.
il y a une infinité de solutions mais on peut fixer arbitrairement le point M par ou passe le pli à trouver MM'
construire les plis MM' et NN' étant donnés A, B, M
(le problème d'origine ne demandait pas de construire mais de calculer le maximum d'un certain angle étant donné seulement l'arc AB)
Cliquez pour afficher
Bonjour
La solution est très jolie et de niveau collège . Personnellement je n'aurais pas tracé le petit cercle ni la bissectrice mais les perpendiculaires en A et B au cercle initial . Le résultat est le même et évite la justification de la concourance des droites sur l'oméga .
J'ai bêtement gardé de vieux réflexes de prof de collège 
Imod
les perpendiculaires au cercle ( = les rayons) ??
tu veux dire sans doute les tangentes au cercle en A et B 
Annuler
connectez vous