Inscription / Connexion Nouveau Sujet
Points acceptables
Bonjour à tous 
En parallèle au fil de Dpi ![]() Des segments tortueux , je propose un nouveau problème dans la lignée de ceux qui ont déjà été proposés cet été , avec des points aux nœuds d'un quadrillage orthonormé .
Des segments tortueux , je propose un nouveau problème dans la lignée de ceux qui ont déjà été proposés cet été , avec des points aux nœuds d'un quadrillage orthonormé .
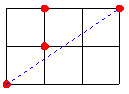
On considère des ensembles de points aux nœuds d'un quadrillage . Un de ces ensembles est acceptable si aucun de ses points ne se situe à égale distance de deux autres . On note n le cardinal de cet ensemble et d(n) la plus grande distance entre deux points de cet ensemble . Pour chaque entier n , on cherche le minimum de c(n)=d(n)² .
Sauf erreur : c(1)=0 , c(2)=1 , c(3)=5 , c((4)=13 , …
On participe dans la bonne humeur et sans blanker 
Imod
PS : il me semble qu'en corolaire on devrait avoir une réponse au problème de Dpi .
salut
*
quelle est la différence avec ![]() Diamètre d'un ensemble varié ?
Diamètre d'un ensemble varié ?
Dans l'exercice précédent on interdisait les distances égales entre deux points quelconques , ici les distances sont prises entre deux paires de points partageant un sommet .
Il est vrai que la nuance est subtile 
Imod
J'ai amélioré c(4)=9 avec les points (0,0) , (1,1) , (1,2) et (3,0) .
Je propose c(5)=17 et c(6)=20 , qui dit mieux ?
Imod
Je donne une illustration pour motiver les troupes :
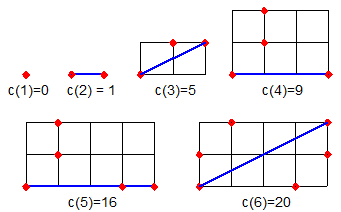
On remarquera que j'ai gagné un point pour c(5) 
Imod
A mon tour de ne pas tout comprendre:
*sur c(5) et c(6) il y a deux fois la distance 1.
*la taille de la grille est-elle limitée à 2 en hauteur?
salut
dpi : l'important n'est pas d'avoir une même distance mais d'avoir de ne pas avoir les mêmes distances à partir d'un même point !! ou encore qu'un (même) point soit équidistant de deux autres.
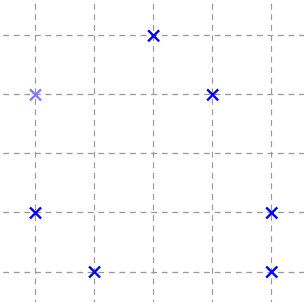
C'est pour ça qu'il est important de bien poser la question . Dans ton fil , si tu refuses deux distances identiques , tu ne feras jamais mieux que l'exemple que j'ai proposé avec neuf segments . Le cadre imposé ici et que je pensais aussi être le tien est qu'un point de l'ensemble ne peut jamais être à la même distance de deux points de ce même ensemble . En fait c'est ce que j'ai répondu à Carpediem qui se posait un peu la même question . Sinon la grille est supposée illimitée , il me semble qu'une forme proche de celle d'un carré devient très vite un bon candidat .
Imod
damned !! j'ai oublié d'effacer la figure : elle ne marche pas à cause du point le plus haut qui est équidistant de deux points ...
ça donne un contre-exemple pour dpi au moins ... 
Avec Carpediem nous avons croisé nos réponses 
Sur sa figure le point tout en haut n'est pas acceptable .
Imod
Il y a encore eu un croisement qui offre un contre-exemple , pas à cause du 2 ou du 9 mais du 13 
Imod
Comme personne n'a émis de réserve pour les premières valeurs de c(n) , j'ai cherché c(7) et j'ai trouvé c(7)=36 :
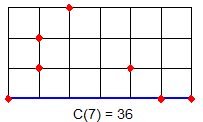
S'il n'y a pas d'erreur cela nous fait sept valeurs et j'ai regardé du côté de l'OEIS et j'ai eu un retour unique ![]()
Le calcul de c(n) se ferait simplement avec la formule où d(k) est le nombre de diviseurs de k . A priori je ne vois pas de rapport direct entre notre problème et cette formule . D'autre part je pensais qu'en ajoutant des points , le champs d'action allait s'approcher d'un carré ce qui ne semble pas vraiment être le cas . Dans tous les cas si la suite de l'OEIS est la bonne , on ne pourra pas mettre plus de 20 points dans la grille de Dpi pour son problème mais comme la forme carrée ne semble pas s'imposer , ça risque d'être bien moins .
Il y a encore du grain à moudre 
Imod
Il me semble qu'on avait déjà compris 
Quelques remarques : ta solution avec 11 points ne fonctionne pas à cause du point D et du point I donc globalement on retrouve une solution à 9 comme celle que j'ai proposé avec des contraintes bien plus fortes . Je n'ai pas essayé de faire mieux pour le moment car je préfère essayer de grimper la colline qui mène à ma boulangerie avant d'attaquer l'Everest . Sinon pour mon problème , la formule de l'OEIS ne peut pas être la bonne car de nombreuses valeurs de la liste ne sont pas sommes de deux carrés . Comme je disais , il y a encore du grain à moudre ici et sans doute là bas .
Imod
En effet , rien ne l'empêche 
En fait j'avais un doute sur l'ensemble des figures . Il ne faut pas hésiter à remettre en cause toutes les propositions car les fausses certitudes dans les cas simples perturbent énormément la suite des recherches .
Je pense que tu viens de lever un point de blocage 
Imod
>BonjourLittlefox
Ton aide est toujours efficace.
Je galère depuis 10 jours sur ma grille 10x10.
Quel est le maximum de segments de longueur différente que l'on peut tracer entre deux noeuds du quadrillage avec la contrainte supplémentaire que tout autre segment traçable entre points retenus soit aussi de longueur différente .
.
@dpi
Désolé mais j'ai vu ce problème en premier et il me semblait plus générique. J'irai voir le tien plus tard, si j'ai encore le temps ^^
J'ai sorti mon Python et fait une recherche exhaustive mais intelligente pour ne pas dépenser du calcul inutilement ^^
J'ai amélioré toutes les solutions après n=4
Sans plus attendre voici mes résultats:
 Cliquez pour afficher
Cliquez pour afficherDu côté de l'oeis, ça ne correspond à rien. J'ai même cassé leur serveur en oubliant un 25

Et voici mon code:
 Cliquez pour afficher
Cliquez pour afficher- Pour chaque solution, on peut définir l'origine sur n'importe quel sommet.
- On peut ordonner les points des solutions par distance à l'origine strictement croissante.
- On peut mettre le second sommet dans le premier octant.
- Pour ajouter un point, il suffit de vérifier les triangles où ce point est un sommet (si on a un triangle isocèle, le point est rejeté).
- On peut donc construire une solution en plaçant les points de manière incrémentale en partant de l'origine.
- Après avoir trouvé une solution:
On peut limiter le rayon par rapport à l'origine du champ de recherche.
On peut rejeter les nouveaux points qui sont trop loin d'un point précédent.
Malgré tout, je parcours potentiellement n fois chaque solution: En mettant l'origine sur chacun des sommets.
Tout cela me dépasse un peu beaucoup , il est vrai que l'exercice est un peu tarabiscoté mais l'OEIS est habitué à bien pire 
Imod
@LittleFox
En représentant les solutions que tu as obtenues jusqu'à n=10 , j'ai noté une certaine régularité dans la disposition des points . Il y a des symétries , des rotations et il semble que les points tendent à se disposer au voisinage d'un cercle . Je ne sais pas si ton programme peut aisément produire des résultats après n=10 , si c'est le cas je suis preneur .
Merci d'avance 
Imod
Je viens de voir que tu avais ajouté n=11 et n=12 . On approche d'un cadre carré mais les points ne sont pas toujours aux abords d'un cercle .
Imod
Mon programme trouve facilement des solutions au delà de n=12 mais ça devient très lent de parcourir toutes les solutions pour garantir la minimum.
Il n'y a pas de garantie que les points se comportent bien.
Pour n=8 et n=10, le minimum est unique et les points forment une figure avec plusieurs symétries. On dirait un cercle déformé.
Pour les autres n, ce n'est pas le cas, il y a plusieurs solutions avec des points plus intérieurs.
Sans garantie que ce soit le minimum, voici des solutions pour n > 12 (j'ai laissé n=20 tourner un peu plus longtemps):
 Cliquez pour afficher
Cliquez pour afficherAucun n'est très régulier. Par exemple ma meilleure solution pour n=20:
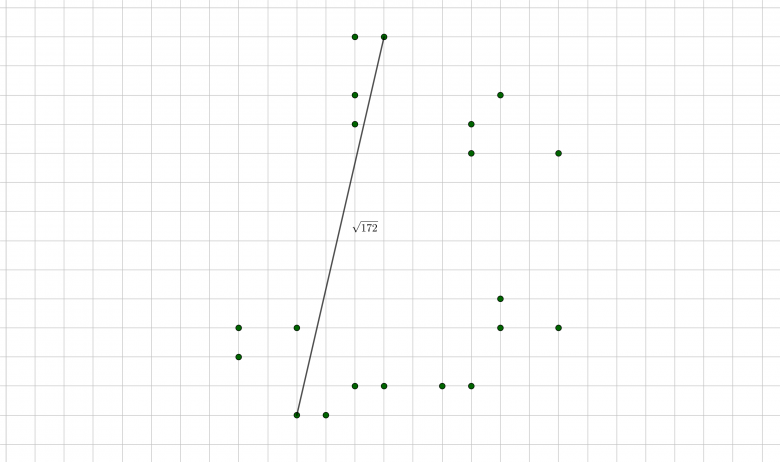
Et voici la liste des solutions minimum pour n <= 10:
 Cliquez pour afficher
Cliquez pour afficherLe code est un peu plus lent car il élimine moins de solution. Je n'ai donc pas la liste pour n=11 et 12.
J'ai retiré les symétries par y=x, les rotations de 90° et les translations.
Au moins ce sujet est résolu ,nous serions heureux si tu résolvais les "segments tortueux" sur une grille 10x10
@dpi
Le problème pour "segments tortueux" ne semble pas bien défini. En tout cas Imod semble y perdre ses cheveux 
Désolé dpi, je ne suis pas tenté pour l'instant. Je suis les updates sur l'autre sujet. Pas besoin de "notifications" ici 
J'ai eu du mal à lire tes longues listes sur mon petit écran mais j'y suis arrivé 
J'ai tout de même remarqué plusieurs choses .
En effet les valeurs ne vont pas s'agglutiner sur un cercle mais elle s'éloigne tout de même du "centre" pour se placer dans une couronne .
Autre chose qui vient peut-être de la façon dont tu as conçu ton programme , il semble qu'à partir d'un moment certaines valeurs ne changent plus . Un peu comme des électrons qui viendraient progressivement remplir les niveaux les plus bas , les autres gardant pour un temps une certaine liberté .
Imod
Oui, ça vient de la façon dont j'ai construit mon programme. Je place en premier sommet, puis le second, puis le troisième, etc et si je ne trouve pas de sommet je reviens sur le sommet précédent.
C'est du "backtracking". Ce n'est pas que les valeurs ne changeront plus, c'est que je vais tester toutes les possibilités avec ce préfixe avant de passer au préfixe suivant.
C'est plutôt comme si tu comptais tous les nombres de 000000 à 999999. Tous les chiffres vont apparaître mais l'ordre dans lequel tu compte fais que le chiffre des unités va changer beaucoup plus que le chiffre des milliers.
D'accord , ça fait penser à la loi de Benford mais ça reste troublant . D'autres idées me sont venues , tu en feras ce que tu voudras 
J'ai d'abord regarder en détail ton c(20) dont les points sont disposés de manière plutôt anarchique . Il y a tout de même une concentration des points dans une couronne . Il faut en fait éviter que les 190 médiatrices rencontrent les points de l'ensemble . Notamment en limitant leur nombre .
Autre chose qui mettrait de côté le tracas des différentes décompositions en carrés . On pourrait poser le même problème avec la distance Manhattan au lieu de la distance classique qui n'a aucune raison de s'imposer sur un quadrillage .
Imod
Bonjour. LittleFox toujours aussi efficace. Bravo. Comme je l'ai déjà dit dans plusieurs problèmes de ce type, au-delà de quelques points, seule une solution informatique peut résoudre ces problèmes. Dans "Points à distances entières", en 1991 on n'avait pas trouvé mieux que 6 points. Peut-être qu'aujourd'hui on pourrait faire mieux avec un bon programme à la LittleFox.
@derny
Woaw, tu ressors des vieux dossiers  En 1991 je n'avais pas 2 ans
En 1991 je n'avais pas 2 ans 
Tu as un lien?
@Imod
Mon programme peut être facilement modifié pour la distance de Manhattan. Mais c'est ce que tu proposes dans ![]() Manhattan robot. Non?
Manhattan robot. Non?
@LittleFox : c'est bien le même problème , quand un exercice part dans un peu dans tous les sens il est parfois bon de repartir de zéro 
Imod




