Proba

 Niveau exercicesPartager :
			        
Proba
Posté par 
flight  22-04-20 à 06:52
Bonjour,

Une urne contient une boule blanche et une boule noire, on y effectue des tirages successifs de la façon façon suivante :

Si on tire une boule blanche, on la remplace par une boule noire, Si on tire une boule noire alors on la remplace par une boule blanche avec une  probabilité p et par une boule noire avec avec une probabilité q. 

(moralité on a toujours 2 boules dans l'urne à la fin chaque étape de tirage). 

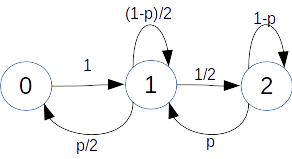
On pose Xn la variable aléatoire égale au nombre de boules noires presentes dans l'urne à l étape n. 

Quelles sont les valeurs prises par Xn ?. 

Quelle est la loi de Xn ? 
 Posté par 
Sylvieg re : Proba  22-04-20 à 11:24
Bonjour,

La première question est facile :
 Cliquez pour afficher
0, 1 et 2.
C'est pour nous mettre en confiance 

Un début pour la seconde question : Cliquez pour afficher
J'ai utilisé les initiales de zéro, un et deux, pour poser

zn = P(Xn=0), un = P(Xn=1) et dn = P(Xn=2).

zn+1 = (1/2)pun

un+1 = zn + (1/2)qun + pdn

dn+1 =  (1/2)un + qdn
 Posté par 
veledare : Proba  22-04-20 à 16:34
bonjour,

X0=1

P(X1=0)=P(X1=2)=1/2

P(X1=1)=0

P(X2=1)=1

et l'on retrouve  la composition initiale

est-ce que l'on n'a pas 

P(X2k=1)   =1

et 

P(X2k+1)=0)=P(X2k+1=2)=1/2
 Posté par 
verdurinre : Proba  22-04-20 à 21:54
Bonsoir,

je ne suis pas vraiment d'accord avec veleda que je salue.

 Cliquez pour afficher
On a une chaîne de Markov dont le graphe de transition est, sauf erreur de ma part :

Ensuite, à l'aide de techniques classiques et de Xcas, je trouve :

 Posté par 
verdurinre : Proba  22-04-20 à 23:09
Et j'ai certainement fait une erreur quelque part.
 Posté par 
veledare : Proba  22-04-20 à 23:48
bonsoir Verdurin,

désolée,, j"ai un très gros problème de vue et j'ai sans doute mal lu le texte malgré ma loupe,j'y reviendeai demain
 Posté par 
Sylvieg re : Proba  23-04-20 à 08:14
Bonjour,

@veleda,

Citation :
Si on tire une boule noire alors on la remplace par une boule blanche avec une  probabilité p et par une boule noire avec avec une probabilité q. 
En majuscules :

"SI ON TIRE UNE BOULE NOIRE ALORS ON LA REMPLACE PAR UNE BOULE BLANCHE AVEC UNE PROBABILITÉ  P  ET PAR UNE BOULE NOIRE AVEC UNE PROBABILITÉ  Q ."

@verdurin, Cliquez pour afficher
Ton graphe de transition est bon.

Après il y a un blème avec la somme des 3 expressions pas égale à 1.

Je ne suis plus assez au point pour traiter mes relations de récurrence  

Par contre je suis capable de vérifier si ce qu'on propose ne comporte pas d'incohérence facile à détecter 
 Posté par 
flightre : Proba  23-04-20 à 14:30
Daccord avec les réponses de Sylvieg 
 Posté par 
flightre : Proba  23-04-20 à 14:31
je trouve pareil ...
 Posté par 
verdurinre : Proba  23-04-20 à 19:33
J'ai refait le calcul en faisant plus attention.

 Cliquez pour afficher
Finalement je trouve, en posant 

Êtes-vous d'accord ?
 Posté par 
Sylvieg re : Proba  23-04-20 à 19:55
Déjà la somme fait bien 1 

Je regarderai demain.
  Posté par 
jandri re : Proba  23-04-20 à 23:09
Bonjour,

ces derniers résultats de verdurin  sont exacts.

Pour les obtenir on peut rechercher les valeurs propres de la matrice qui apparait dans le message de Sylvieg du 22-04-20 à 11:24 : 1 est valeur propre de la transposée et les deux autres valeurs propres se calculent aisément avec la trace et le déterminant. Cela permet d'écrire le vecteur donnant la loi de  sous la forme :

 Cliquez pour afficher
 avec 

On en déduit que la loi de  a une limite que l'on peut alors calculer aisément à partir des relations données par Sylvieg. 

 Cliquez pour afficher

Pour obtenir la loi de  il reste à résoudre un système de deux équations à deux inconnues.

Sans calculer la loi de  on peut calculer son espérance à partir des relations données par Sylvieg. En effet, cette espérance vérifie une relation de récurrence très simple :

 Cliquez pour afficher
 avec 

On en déduit E et sa limite :

 Cliquez pour afficher
 et