Inscription / Connexion Nouveau Sujet
proba
Bonsoir
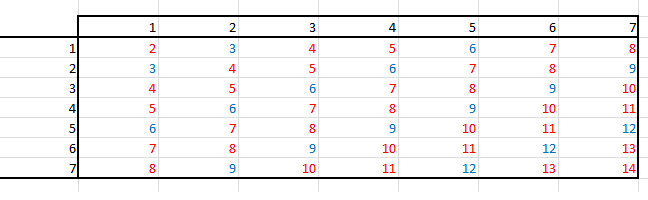
je vous propose l'exercice suivant : on se donne les entiers allant de 1 à n et on choisit parmi ces entiers deux entiers au hasard (prélèvement avec remise ; les entiers choisis peuvent être égaux ) on les nommera X et Y comment étant des variables alétoires.
Quelle est la probabilité que X + Y soit un multiple de 3 ?
Bonjour,
Ma réponse ne comptait pas les doublons du genre 1+5 ;5+1.
En gardant la méthode de candide 2 on arrive à une tendance simple:-->1/3
Bonsoir flight.
Je ne suis pas d'accord avec ta réponse.
Prenons par exemple n=2 : on a alors
P(X+Y=2)=1/4
P(X+Y=3)=1/2
P(X+Y=4)=1/4
Il me semble difficile de dire que la probabilité pour que X+Y soit un multiple de 3 est 1/3.
Mais il est clair que quand n tend vers l'infini la probabilité tend vers 1/3.
@candide2
on trouve les mêmes résultats mais bien entendu je trouve ma présentation meilleure que la tienne, j'imagine que tu es dans le cas inverse 
Bonjour verdurin,
@candide2
on trouve les mêmes résultats mais bien entendu je trouve ma présentation meilleure que la tienne, j'imagine que tu es dans le cas inverse.
Tout à fait 
Bonjour Verdurin ,daccord avec ta remarque , merci ....
j'ai obtenu la formule generale suivante :
P(X+Y=0[3]) =  (3j-1)/n² +
(3j-1)/n² +  (2n-3j+1)/n² , la premiere somme va de j =1 à E((n+1)/3) , la seconde somme va de j=E((n+2)/3) à E(2n/3).
(2n-3j+1)/n² , la premiere somme va de j =1 à E((n+1)/3) , la seconde somme va de j=E((n+2)/3) à E(2n/3).
si n =2 on obtient P(X+Y=0[3]) =  (3j-1)/4 +
(3j-1)/4 +  (5-3j)/4 , les bornes vont de j=1 à 1 ce qui donne 2/4+2/4 = 1/2 .
(5-3j)/4 , les bornes vont de j=1 à 1 ce qui donne 2/4+2/4 = 1/2 .

 Cliquez pour afficher
Cliquez pour afficher