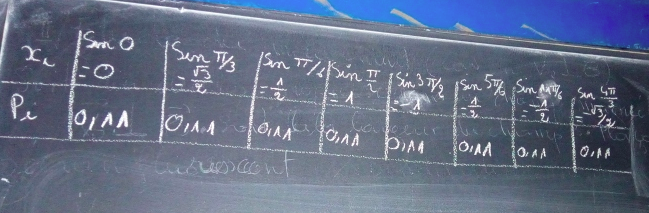On joue avec deux dés cubiques non pipés.
Les faces de l'une sont marqués : 0,0,pi/3,pi/3,4pi/3,4pi/3.
Les faces de l'autre : 0,0,pi/6,pi/6,pi/2,pi/2.
On lance les deux dés simultanément. On appelle alpha et bêta  les deux nombres qui apparaissent sur les faces supérieures, et on appelle X la variable aléatoire qui à chaque lancé associe le réel sin(α+β).
1.quelles sont les valeurs prises par X ?
2.Etablis la loi de probabilité de X, et calcule son espérance mathématique.

Pour commencer j'ai d'abord Ressencer dans un tableau les sommes possibles .ensuite sin(α+β) m'a donné sin(0) ,sin(pi/3),sin(pi/6),sin(pi/2),sin(3pi/2),sin(5pi/6),sin(11pi/6),sin(4pi/3)   qui sont les valeurs prises parX.
Pour la loi de probabilité voici mon tableau