Bonjour

En effet il faut la proportion de cellule anormales !
cela peut sans doute se calculer par une loi binomiale

Mais du coup, l'indépendance des épreuves successives dépend de la taille du lot
Si tu as un lot de 100 cellules alors c'est trop petit pour qu'on puisse considérer les épreuves indépendantes et identiques
Si tu as un lot de 2098293829 cellules la différence est négligeable
A moins que tu effectues des tirages avec remise

Il suffit donc de calculer la probabilité d'en trouver au moins 3 anormales sur 20
Soit X la variable aléatoire prenant comme valeur le nombre de cellules anormales observées sur 20 essais avec une probabilité de p

P(X3) = 1 - P(X2) ce qui se calcule très facilement avec une calculatrice de lycée en tapant 1-binomFrep(20,p,2)

Ou pour être plus rigoureux,  

Je reviens sur ce que j'ai dit:
Si tu as un lot de 100 cellules et tu n'effectues pas de remise, les épreuves ne peuvent pas être considérées comme indépendantes et identiques donc il n'y a pas de loi binomiale
Donc tous les calculs "simples" que j'ai mis ne peuvent pas être appliqués

Tout d'abord, merci pour les réponses.
Dans l'hypothèse (malheureuse) que la proportion de cellules anormales est pile au seuil de la maladie c'est-à-dire 3/30, je pense qu'on pourra estimer le seuil MINIMAL ACCEPTABLE du nombre de cellules à observer.

Donc considérons cette proportion à 3/30 (=10%). Pouvez-vous m'expliquer le cheminement (éventuellement la réponse) pour répondre à ma question ?

Il n'y a pas de remises, car évidement, nous faisons en sorte de ne pas observer deux fois la même cellule.
Il y a au moins 400 cellules observables. L'enjeu, c'est justement de se demander, au bout de combien de cellules observées on peut raisonnablement s'arrêter pour être sûr à 95% que le seuil des 10% ne sera pas atteint.

Bonjour,
d'après ta description le nombre de cellules anormales suit une loi hypergéométrique.

La probabilité de n'observer aucune cellule anormales en k observations est égale à



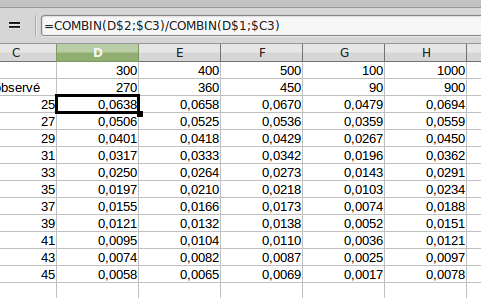
si il y a 400 cellules observables.
Si le nombre de cellules observables est N on remplace 400 par N et 360 par 0,9*N.

C'est facile à faire sur un tableur.

Ensuite on applique le principe des tests statistiques :
si
   on n'a vu aucune cellule anormale
et que
   la probabilité de cette observation sous l'hypothèse qu'il y a 10% de cellules anormales est inférieure au seuil de risque
alors
  on rejette l'hypothèse « il y a au moins 10% de cellules anormales ».

Je rajoute une image de mon tableur,
la première ligne donne le nombre de cellules observables.

Je pense que la notion de risque et de seuil n'est pas importante pour moi pour l'instant.

Je ne suis pas sûr que, Verdurin, tu aies bien compris mon "problème".
Je vais essayer de m'exprimer mieux.

Il y a 400 cellules. 40 sont anormales.
J'en ai regardé 10 et aucune n'est anormale.
Dans les 20 prochaines observations, quelles sont mes chances d'en trouver au moins 3 d'anormales ?

Peut-être qu'il faudrait que je réfléchisse à la probabilité inverse pour que ce soit plus simple (et à la fin je ferai 1-...)

Il y a 390 cellules, et 40 sont anormales parmi les 390 (j'en ai déjà tiré 10 qui étaient normales, et il y a en tout 40 anormales et 360 normales, car 10% d'anormales).

Je vais en tirer 20 parmi ces 390 restantes.

Et comme je l'ai dit au début, je fait :
1-
(Proba d'en trouver 1 anormale ?
+Proba d'en trouver 2 anormales ?)

En utilisant la loi hypergéométrique , ou presque.

Il te reste 390 cellules dont 40 anormales.
Tu tires 10 cellules au hasard parmi 390, il y a possibilités.
En tirer au moins trois anormales est le contraire d'en tirer zéro, une ou deux.

La probabilité cherchée est donc

C'est exactement ça Verdurin ! J'ai retrouvé la formule sur wikipédia https://fr.wikipedia.org/wiki/Tirage_(math%C3%A9matiques) et testé en changeant des paramètres.

salut

à verifier  ..peut etre en utilisant la loi de poisson
dans  400 cellules normales  on observe  40 cellules anormales
dans 420 cellules normales  on observe  42 cellules anormales

et prenant =42  on calcul P(X3, =42) = 1 - [ P(X=0)+P(X=1)+P(X=2)]   avec

P(X=k)= e^-42.^k/k!

je retire ce que j'ai dit .. ca manque de rigueur ...

Oups,
j'ai fait le calcul avec l'observation de 10 cellules et non 20.

En tirant encore 20 cellules, la probabilité d'en observer au moins trois anormales est



Avec mes excuses.

re... en reprenant ma piste ce serait plutot

avec    400 cellules normales  on observe  40 cellules anormales   on cherche la proba d'en voir au moins  43  sur  420 cellules

et prenant =42  on calcul P(X43, =42) =
1 -     e^-42.42^k/k!  k compris entre 0 et 42

ce qui donne  1- 0,6009 = 0,391

Salut flight.

salut Verdurin

pas d'inquiete je n'etais pas entrain de peindre sur ton mur , j'ai consideré le  probleme comme etant "ouvert" avec un enoncé un peu bricolé

Rebonjour à tous

Verdurin, en utilisant la loi binomiale comme je l'avais suggeré au tout début je trouve un résultat proche de celui que tu trouves avec la loi hypergéométrique, à savoir 0.32307 contre ton 0.337

Cette différence est-elle due à la petite taille de l'échantillon qui rend la loi binomiale inadaptée?

Ces résultats sont pratiquement égaux.
Et c'est normal.
J'ai donné un point de vue théorique mais, quand on a un taux de prélèvement assez faible, la différence entre une loi binomiale et une loi hypergéométrique est négligeable.

En d'autres termes, il n'y a pas de différence appréciable entre un prélèvement avec ou sans remise quand on prend un échantillon de taille 20 dans une population de taille 400.