R² est un ensemble
R²= { (x;y) / x R, yR}

Merci pour ta réponse. Donc il n'y a qu'un ensemble, que je peux représenté comme cela alors :



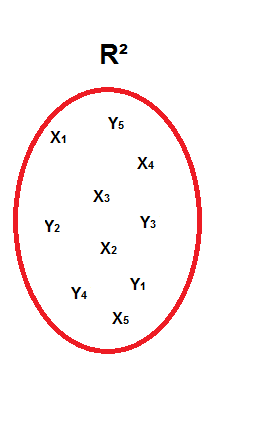
et non pas :

Perso j'aurai pensé que c'était la 2ième image qui représentait R².

Bonjour,

Absolument pas. est un ensemble de couples, , etc.,  ordonnés   si

Ok merci pour ta réponse.

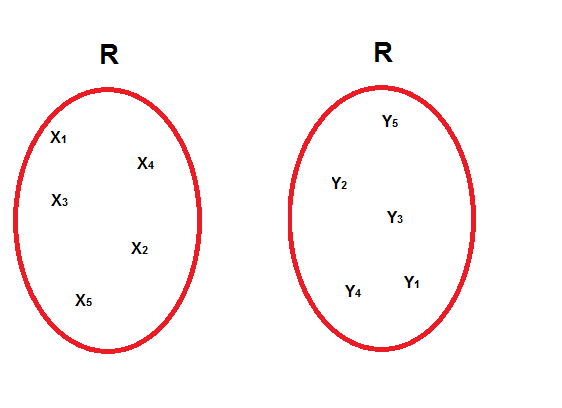
Mais quand on a un ensemble E composé de x et un autre ensemble composé de y on est bien d'accord que le produit cartésien de ces 2 ensembles c'est le couple (x,y) donc je pensais qu'il en était de même si on avait RxR.
Donc tu me confirmes que c'est la première image qui est la bonne ?

Mais quand on à un plan cartésien l'axe des abscisse représente bien un ensemble R et l'axe des ordonnées un autre ensemble R donc si on fait le produit cartésien c'est l'association des 2 ensembles donc on à bien 2 R distincts même si ils de même nature donc R .

Si je comprends bien ce que tu ma dit en fait il y a un seul unique ensemble R on peut pas en avoir 2 comme sur ma 2 ième image ?

Désolé si je me répète ou que je ne prends pas acte tout de suite de ce que tu me dis mais c'est surtout pour moi pour bien comprendre qu'il n'y ai pas de doute dans mon esprit.

Merci.

Bonsoir
Il n'y a qu'un IR, mais IR² n'est pas IR

on ne représente pas IR comme une "patate", mais sous forme d'un axe gradué
on représente alors IR² comme le plan, chaque point correspondant via le choix d'un repère à un couple (x,y) de réels
même pour un produit AxB, on ne le représente pas comme deux patates côte à côte, mais comme un graphe, les éléments de A sur un axe, ceux de B sur un autre , et les éléments de AxB comme points du plan (ou cases d'un quadrillage quand A et B ont peu d'éléments, représentés par des segments sur les axes)

@lafol super merci pour ta réponse qui est bien claire, tu as dissipé un brouillard que j'avais dans la tête à se sujet.

Salut.