Inscription / Connexion Nouveau Sujet
Produit scalaire Carré
Bonjour, je bloque lors de la première question et il m'est impossible de continuer sans celle ci. Voici l'énoncé:
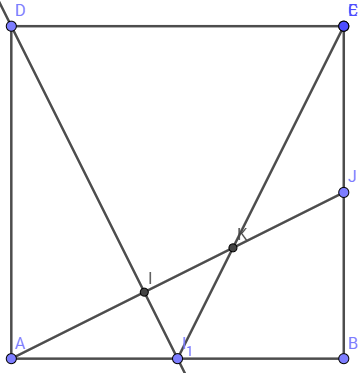
ABCD est un carré de côté 1, les points I et J sont les milieux respectifs des segments [ab]
et [bc]. H est le point d'intersection de la droite (aj) et de la perpendiculaire à la droite (aj)
passant par d, k est le point d'intersection des segments [aj] et [cj].
1) En exprimant de deux façons le produit scalaire AJvecteur.ADvecteur, calculer la longeur AH.
2) En utilisant le produit scalaire AJvecteur.CIvecteur, determiner la valeur approchée à 0,1° près par excès de la mesure de l'angle JKI.
Mes reponses:
1) AJvecteur . Advecteur = AJvecteur . AHvecteur car H projete de D sur AJ.
AJ²=AB²+BJ²=1.25 soit AJ=Racine carré de 1.25
Voila je suis bloquer à ce point point ci de l'exercice, merci d'avance de votre aide...
1) AJvecteur . Advecteur = AJvecteur . AHvecteur car H projete de D sur AJ.
AJ²=AB²+BJ²=1.25 soit AJ=Racine carré de 1.25
Voila je suis bloquer à ce point point ci de l'exercice,
AJvecteur . Advecteur = AJvecteur . AHvecteur =AH*AJ
tu bloques pour AH?