Inscription / Connexion Nouveau Sujet
Quadrilatère
Bonjour pouvez vous m'aider svp. Merci a tous.
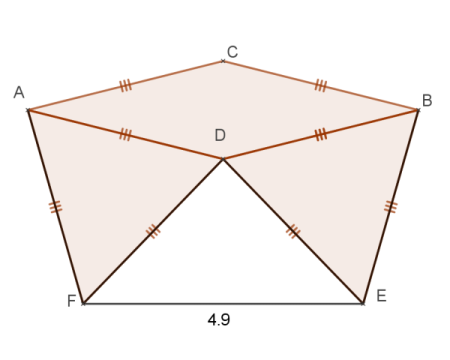
Le quadrilatère ACBD est un losange de 3,5cm de côté.
Les triangles ADF et BDE sont equilateraux.
1) coder la figure.
2)Quelle est la nature du triangle FDE ? Justifier.
3)FE=4,9cm.
Calculer le périmètre du polygone ACBEF.
2 )Le triangle FDE est isocèle car il a 2 côtés egaux.
3) p=(3, 5*4)+4,9=28,9cm
Le périmètre est de 28,9cm.
Bonsoir,
D'où sort cette mesure fausse ?
3)FE=4,9cm
A l'avenir évite de mélanger l'énoncé et tes réponses...
Montre nous ta figure et si besoin précise l'énoncé qui doit être rigoureusement et complètement mis sur le site....
A titre exceptionnel et puisque tu as déjà saisi l'essentiel de l'énoncé, mets une copie de l'énoncé qui t'a été donné (scan ou photo).
Ensuite montre nous la figure que tu as réalisée.
Il y a manifestement... un bug 
Tu as devancé ma demande d'énoncé 
Il nous manquait la figure !!
Il manque un bon morceau de l'énoncé : tourne ton appareil photo...
Ceci étant mon losange n'est pas compatible avec la figure de ton énoncé ; d'où mon incompréhension.
Je vais aller "écraser" mon losange et le rendre compatible avec cette mesure de FE qui arrive après coup...
Avec la figure de l'énoncé, on s'aperçoit qu'une construction conforme à celle donnée doit se construire à partir du segment [FE] de longueur 4,9.... sinon il y a une infinité de losanges possibles si on ne tient pas compte de cette contrainte.
Bon donc tout s'arrange....
sauf ton calcul :
3) p=(3, 5*4)+4,9=28,9cm
Corrige vite cette grosse erreur et... bonne soirée
 .
.
Oui ! encore faut-il le DEMONTRER...
Comment démontrer que les droites (AB) ET (FE) sont parallèles ??
Pense quand même à dire que les droites (AB) et (FE) te semblent parallèles et que si tel est le cas (ce qu'il faudrait démontrer !!!), alors effectivement le quadrilatère ABEF est un trapèze (on peut même alors préciser que ce trapèze est un trapèze isocèle car ses cotés non parallèles sont égaux  )
)
bonjour
Comment démontrer que les droites (AB) ET (FE) sont parallèles ??
je me posais la même question.
Avec les angles alternes/internes?
avec (CD) axe de symétrie de la figure ?
je n'y suis pas arrivé et vous?
Une démarche possible…
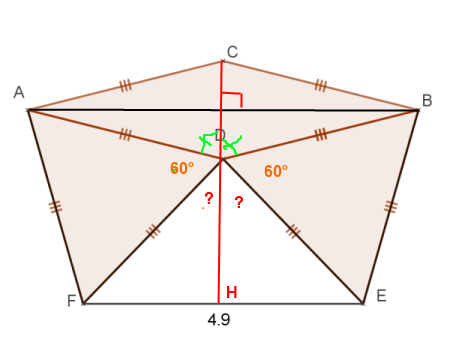
On appelle H le point d'intersection de (CD) avec (FE). Objectif : montrer que le segment [DH] est la hauteur issue de D dans le tr isocèle DEF.
Dans le losange ADBC, les diagonales se coupent en leurs milieux et sont perpendiculaires. Les angles ADC et CDB sont égaux.
On démontre que les angles FDH et HDE sont égaux (180° -60°- ADC)
Dans le tr isocèle EDF, l'égalité des angles FDH et HDE permet de dire que [DH] est la bissectrice de l'angle EDF. Or dans un tr isocèle la bissectrice issue du sommet est aussi hauteur, médiatrice de la base. Donc (CD) est perpendiculaire à (FE).
La droite (CD) est perpendiculaire aux droites (AB) et (FE) donc je te laisse conclure…
C'est un peu lourd mais je pense correct….
Si des collègues ont d'autres démonstrations….
Bonjour,
sans formalisme excessif,
il est clair que (CD) est axe de symétrie du losange ACBD
et que les segments BE et AF sont image l'un de l'autre dans cette symétrie (mêmes longueurs, mêmes angles avec le losange )
donc (CD) est axe de symétrie ( = médiatrice) de EF
donc (AB) et (EF) perpendiculaires à (CD) ...
d'ailleurs
avec (CD) axe de symétrie de la figure ?
zedmat j'avais essayé d'utiliser les angles.
[DH] Est la médiatrice de [FE] MAis je n'arrivais pas à prouver que C Det H alignés.
D'ailleurs est ce que tu as prouvé toi, cet alignement ?
Relis bien ce que j'ai écrit :
Dans ma démonstration (celle de Mathafou est plus... légère  ),
),
[DH] n'est PAS la médiatrice de [EF].... et toute la démarche faite avec les angles, a pour but ultime justement de démontrer que [DH] est la bissectrice donc la hauteur donc la médiatrice issue de D dans le tr isocèle...
On appelle H le point d'intersection de (CD) avec (FE). Objectif : montrer que le segment [DH] est la hauteur issue de D dans le tr isocèle DEF.





