salut,
soit G cette primitive
F(x)=G(2x)-...

G(2x) - G(x) et ensuite?

derive cette expression

jai pas bien compris il faut que je dérive G(2x)-G(x) alors que je connais pas G?

oui mais tu connais G'
c'est suffisant

Je ne vois pas ce que je dois faire :/ ce que je sais c'est que F'=f

G est une primitive de t->1/ln(t)
donc G'(t)=1/ln(t)
donc G'(x)=1/ln(x)
Calcule la derivee de G(2x), attention au piege !

G'(2x)= 1/ln(2x) ?? non jpense pas

ce qui me perturbe c'est de ne pas connaitre G(x) comment à partir de sa dérivé je la trouve? :/

Disons qu'on a la dérivé de G'(2x)-G'(x) à quoi elle correspond? nous ce qu'on veut c'est G(2x)-G(x)

Bonsoir,

Non ! L'on a sur



comme attendu.

Merci ThierryPoma pour votre réponse mais est ce que vous pouvez m'expliquer pourquoi on a fait 2G'(x)-G(x) svp?

Soit une fonction dérivable sur . Alors, posant , l'on a .

bonsoir,

j'ai une question à propos l'encadrement d'intégrale

Soit F la fonction définie sur [1;+∞[ par:




1)a) Exprimer F à l'aide d'une primitive sur ]1;+∞[ de la fonction



En déduire que F est dérivable sur ]1;+∞[

et que F'(x)=

---> déja fait.

b) en deduire les sens de variations de F

---> decroissante sur ]1;2] et croissante sur [2;+∞[

2)a) Déterminer le sens de variation de f sur ]1;+∞[

-->decroissante sur ]1;+∞[

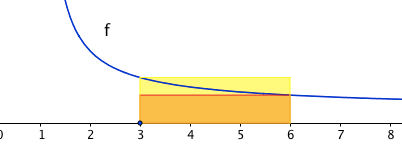
b) En deduire l'encadrement   pour tout

--> je bloque ici:

je sais que si pour tout x de [a;b] , f(x) < g(x) alors

pour commencer, faut-il encadrer t de cette manière?




pour ensuite construire la fonction f? et prendre l'intégrale de chaque côté?

j'ai essayer ça:



Donc:

je sais que c'est faux.. la question dit en déduire donc il faut déduire quelque chose de la variation de f sur ]1;+∞ [ parceque F'=f ?? et que dois-je en déduire pour trouver l'encadrement attendu?

Merci

*** message déplacé ***

je me suis trompé au lieu de a et b je voulais marquer x et 2x

*** message déplacé ***

svp ^^

*** message déplacé ***

Salut,

Comment as-tu calcule F'(x) ?

*** message déplacé ***

il faut continuer dans le meme fil Question sur intégrale

*** message déplacé ***

malou ***car toutes les questions d'un même problème doivent être posées au sein du même sujet sur le site. Merci****

TheMathHatter

F(x)= G(2x) - G(x) avec G une primitive de

donc G'(x)=

F'(x) = 2G'(2x)- G'(x) et on trouve à la fin le résultat attendu

Oui je viens de voir qu'on t'avait deja donne la reponse. Evite le multipost qui fait perdre du temps a ceux qui t'aident.

Quelqu'un peut me guider pour la 2)b) ?

je sais que f est décroissante:



en prenant l'intégrale de chaque coté on trouve:



mais comment calculer =

car on peut pas trouver une primitive directement de non?

tu termines