Question n°1 :
g est un quotient de fonctions dérivables sur  ℝ,  le dénominateur x² - 1  ≠  0 donc :
(x - )(x+ )  ≠  0 sur E,  donc g est dérivable sur E

Question n°2:
g(x) =
g'(x) =
Je suis pas sur pour la dérivée

je la calcule et je reviens

je trouve comme toi...   tu peux continuer  

Question 3 :
g'(x) a le même signe que -3x² - 3 puisque (x²-1)² est toujours positif vue que c'est un carré
Δ  = -4*-3*-3  = -36
Δ < 0 le polynôme n'admet pas de racine réel

Donc le polynôme -3x² - 3 a le même signe que le coefficient de x² sur   ℝ.
g'(x) est négatif sur E

oui, le dénominateur est toujours positif sur E

pour le numerateur, ce que tu écris n'est pas faux mais je préfère ceci :

-3x²-3  =  -3(x²+1)    
x² +1   est toujours positif    donc .....

x² + 1 est toujours positif donc multiplier par -3 c'est toujours négatif
g'(x) est négatif sur E
Pour la question 3
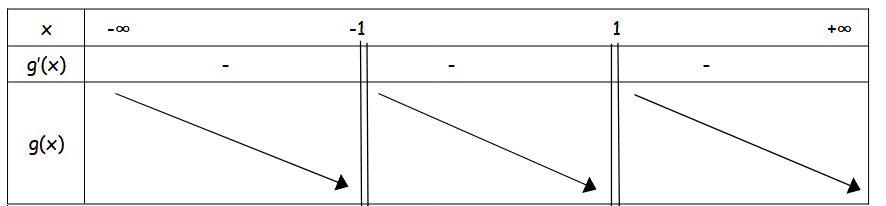
voici mon tableau de variation

Question n°4:
Oui car si g'(x) est négatif sur E alors g(x) est décroissante sur l'ensemble E.

je ne suis pas d'accord avec ton tableau.
IL y a deux valeurs interdites ==> note les avec des doubles barres.
tu ne dois pas traverser les doubles barres.

Comme ca c'est mieux

oui, c'est beaucoup mieux !
à présent, que penses tu de la question 4 ?

Question n°4:
Oui car si g'(x) est négatif sur E alors g(x) est décroissante sur l'ensemble E.

en étudiant la fonction inverse  f(x)= 1/x
tu as dû voir qu'elle est définie sur R - {0}, et elle est décroissante  sur  ]-oo ; 0[   et   sur  ]0 ; +oo[

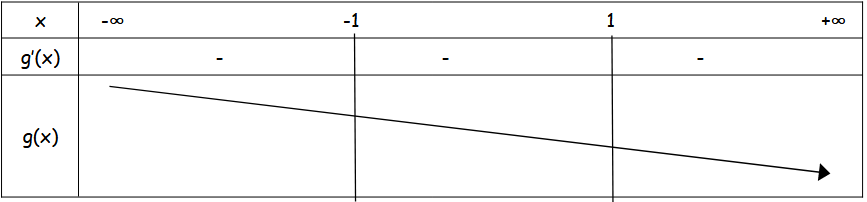
ici, pour moi, c'est mieux de dire qu'elle est décroissante sur chacun des 3 intervalles. Ce qui est logique, puisqu'on a dessiné 3 flèches.  

Bonjour à vous deux

Frexs peux-tu me dire avec quoi tu fais tes jolis tableaux de variations ? Un site ? Et si oui lequel stp ?

Bonjour
Je fais mes tableau de variation sur libre office
en  créant un nouveau tableau.  en cliquant sur tableau insérer tableau
Les flèche en faisant insertion, forme puis flèche
Les lignes en faisant insertion, forme puis ligne
pour les nombre dans la rangé f(x) soit insertion zone de texte
soit insertion cadre (pour des nombres compliqué avec racines ou fracton) puis dans le cadre alt +maj+e
Pour enlever les contour  du cadre clic droit dessus , propriété dans l'onglet bordure, sélectionner le premier préréglage

Eh bien franchement bravo à toi

Bonjour,
Oui, Frexs, tes tableaux sont vraiment jolis.
Cependant la manière dont tu places les flèches dans le dernier prête à confusion.
Je te propose de calculer g(-2), g(0) et g(2) pour comprendre pourquoi on ne s'autorise à parler de fonction croissante ou décroissante que sur un intervalle.

g(-2) = - 1
g(0) = 1
g(2) = 3
Donc  g(x) est décroissant sur les intervalles ]-∞;-1[ ,  ]-1;1[ et ]1;+∞[

Donc les flèche doivent être comme ça ?

oui, TB !

Bonsoir malou,

L'assistant Latex de l'ile permet de faire des tableaux de variations assez facilement, exemple

Bonjour fph67

Oui, je sais , c'est moi qui l'avais demandé en son temps au développeur ? mais j'avais vu que celui posté ici n'en était pas un, et comme je suis à la recherche de code susceptible d'être collé dans overleaf par exemple, qui fasse de belles flèches, etc ...
Bonne soirée

J'ai aussi découvert un jour le site suivant :

Il est assez lourd en ce qui concerne l'utilisation car il faut copier le code Latex et le rentrer dans un autre document mais le résultat est très satisfaisant.
Bonne soirée également.

Merci fph67 , je regarde ça demain depuis l'ordi, ça peut aider effectivement