Inscription / Connexion Nouveau Sujet
Rotations et translations du plan
 Ramanujan
RamanujanBonsoir,
On se place dans un plan euclidien orienté muni d'un repère orthonormé direct.
Soit un nombre réel non congru à
modulo
,
un point de
. La rotation de centre
et d'angle
est notée
Soit un vecteur de
. La translation de vecteur
est notée
I/ Soit un nombre complexe de module 1 et
un nombre complexe. On considère l'application
de
dans lui-même qui a tout point d'affixe
associe le point d'affixe
1) Montrer que si alors
est une translation dont on précisera le vecteur.
J'ai fait : donc
est la translation de vecteur d'affixe
.
Comment je peux déterminer le vecteur 
donc
avec
le vecteur d'affixe
Ma réponse : est la translation de vecteur d'affixe
est-elle la réponse attendue ?
Je mets la suite :
2) On suppose dans cette question que
a) Montrer que possède un unique point fixe
d'affixe
Je trouve facilement :
b) Montrer que l'image par du point
d'affixe
est le point d'affixe
J'ai fait :
On a
Donc :
c) Montrer que est une rotation dont on précisera le centre et l'angle.
Je bloque pour cette question car d'après le cours, une similitude est la composée d'une homothétie et d'une rotation.
Je ne comprends pas ici pourquoi on doit montrer que c'est une rotation.
erreur de recopie dans la question b
que vaut le module de a ?
exprime vec M' en fonction de vec
M' en fonction de vec  M
M
(j'aurais parié sur les questions ! c'est le cours sur les complexes qu'on faisait en terminale et qu'on peut encore faire)
Oui le début mais après ça se complique. J'ai trouvé la question finalement.
est un nombre complexe de module égal à 1. Il est donc non nul. Il admet ainsi une forme trigonométrique :
où
désigne un argument de
Ainsi :
est donc la rotation de centre
d'affixe
et d'angle
qui désigne un argument de
.
Je réfléchis à la suite, j'aurais sûrement besoin de votre aide.
III/ Soient tels que
Soient
On considère l'application , respectivement
, du plan dans lui même, envoyant le point d'affixe
sur le point d'affixe
, respectivement
1/ Soit . Pour tout point
d'affixe
, calculer l'affixe de
.
Je trouve :
2/ Montrer que est une translation ou une rotation.
Si alors
est la translation de vecteur d'affixe
Pour la rotation je bloque 
III-2 : une fois que tu auras la bonne expression de f, tu verras qu'elle est du type "az+b" avec |a|=1
il te suffit d'appliquer ce qui est fait dans la partie précédente pour conclure ! on n'en demande pas plus 
Je corrige :
Notons : où
et
Si
est la translation de vecteur d'affixe
Si :
possède un unique point fixe
d'affixe :
est donc la rotation de centre
et d'angle
où
désigne un argument de
pour
IV/
Soit la rotation d'affixe
et d'angle
et
la rotation de centre d'affixe
et d'angle
.
Déterminer la nature et les éléments caractéristiques de et
Je trouve et
Donc et
est la translation de vecteur d'affixe
C'est juste ?
Dernière question de la première partie.
On considère l'ensemble formé des rotation de
et des translations de
. Montrer que
est un groupe pour une loi que l'on précisera.
Déjà la loi c'est évident que c'est la composition des applications.
Je dois montrer que est une loi de composition interne.
La composition de 2 translation est une translation, la composition de 2 rotations est une rotation. La composition d'une rotation et d'une translation je ne sais pas 
Je ne vois pas comment utiliser les résultats précédents.
D'accord merci.
La loi est une loi de composition interne car si on prend 2 éléments de
et qu'on les compose on obtient un élément de
d'après les questions précédentes.
La loi de composition des fonctions est associative.
Il existe un élément neutre : c'est l'application
Tout élément de admet un inverse. Comment le déterminer ?
En fait je n'ai pas compris pourquoi tout élément de s'écrit sous la forme :
f(z) = az + b avec |a|=1
On a pas démontrer l'équivalence on sait juste que :
(f(z) = az + b avec |a|=1)
est une rotation ou une translation
Puis pour calculer l'inverse :
Si :
donc l'inverse est
(translation)
Si : l'inverse est :
(rotation)
Pour une rotation de point fixe W tu prends un point au pif du plan A daffixe a different de W
Alors ||WA|| = ||WA'|| ce qui se traduit comment avec lecriture complexe?
La question étant terminée je mets la suite qui me pose problème.
Soit une droite de
. La symétrie orthogonale d'axe
est notée
Si et
sont 2 vecteurs non nuls de
, on note
l'angle orienté de
et
.
VI/ Soient et
2 droites sécantes du plan en un point
. On désigne par
et
des vecteurs directeurs de
et
respectivement.
1/ Montrer que est un point fixe de
.
Je ne vois pas comment faire.
Bon ecoute Ramanujan entre ta derniere reponse et ta question il y a 10 minutes qui se sont écoulées. Tu enlèves le temps qui sest passé pendant que tu redigeais la question tu as du passer au bas mot 2 minutes à reflechir
A QUOI CA SERT CE QUE TU FAIS?
J'ai jamais eu de cours de géométrie là dessus, je ne vois pas par où commencer à réfléchir, c'est du chinois.
Oui mais on sait rien sur les droites c'est trop théorique.
Il faut déterminer les coordonnées de leur point d'intersection ?
Une symétrie orthogonale je connais mais je sais pas exprimer par exemple.
Ah merci en effet c'était pas difficile ! Un point qui appartient à une droite est invariant par la symétrie orthogonale par rapport à cette droite.
Ainsi :
Donc
Je bloque sur la suivante.
Soit un point de
distinct de
. Soient
et
Montrer que les angles et
sont égaux.
J'ai une idée. D'après la relation de Chasles et avoir fait un dessin on a :
D'où :
Soit :
Or :
Donc :
Bizarre je trouve pas le résultat voulu 
J'ai fait un dessin mais j'utilise pas le fait que le triangle est isocèle.
D'après la relation de Chasles :
Par ailleurs :
D'où :
Soit :
Ainsi :
Enfin :
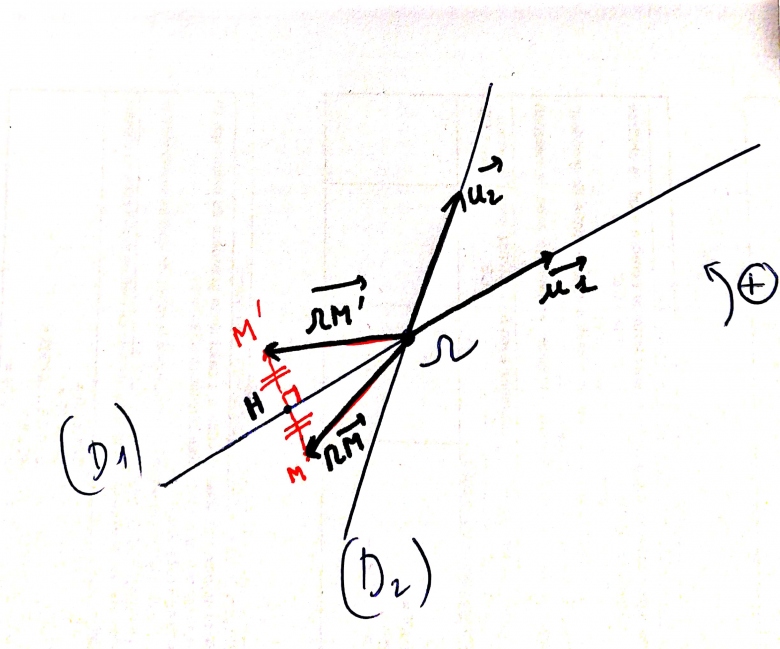
Tu utilises chasles nimporte comment dans ta 2e ligne.
Tfacon tout raisonnement qui nutilisera que des propriétés sur les angles orientés sans prendre en compte quil y a des égalités de distances dues à la reflexion orthogonale sera fausse!
Ramanujan
tu te procures un bouquin de math "TS math" ou "TC" des années 90 et tu auras le cours détaillé sur le sujet (isométries du plan / traduction complexe) ... ça évitera ces
Si j'écris l'égalité des distances, en quoi ça va m'aider pour déterminer une relation entre des angles orientés 
A moins d'utiliser les arguments de nombres complexes, mais on a pas de nombres complexes ici.
quel chantier, une fois de plus ! tu as lu la question ?
est bissectrice du triangle
donc
et comme est colinéaire à


 "
"
 géométrie en post-bac
géométrie en post-bac