Inscription / Connexion Nouveau Sujet
Six points cocycliques
Bonjour,
Pour ceux qui ne connaissent pas :
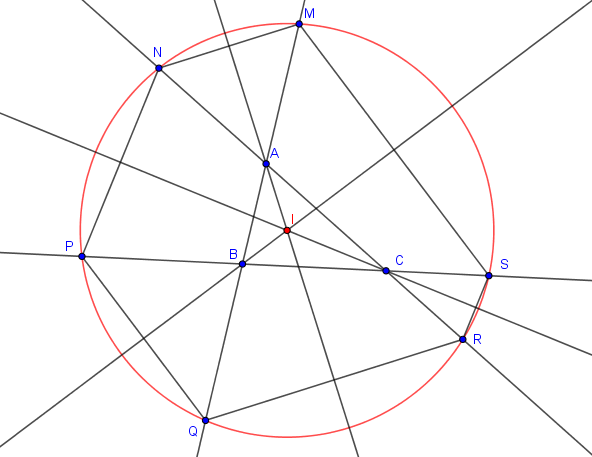
Dans la figure ci-dessous, ABC est un triangle quelconque.
AM = AN = BC.
BP = BQ = CA.
CR = CS = AB.
Démontrer que les points M, N, P, Q, R et S sont cocycliques.
Pensez à blanker 
Ce qui est bien dans cette rubrique "détente" c'est qu'on peut y voir des problèmes apparemment très scolaires prenant toute leur saveur hors contexte . C'est aussi un peu le principe des olympiades ou des rallyes maths mais avec un chrono .
En bref , j'aime bien ce petit coin 
Imod
Réciproque  :
:
Soit un triangle ABC de coté abc de demi-périmètre s=(a+b+c)/2
On trace son cercle inscrit de centre o
on calcule son rayon r avec r²=(s-a)(s-b)(s-c)/s
on trace une tangente (perpendiculaire à ce rayon ) de dimension s
on calcule  (r²+s²)=R
(r²+s²)=R
Le cercle de centre o et de rayon R est tel que les cordes formées
par le prolongement des cotés de ABC sont égales et mesurent a+b+c
Bonsoir,
@dpi,
Je ne vois pas à quel rayon est perpendiculaire la tangente dont tu parles.
Je pensais à une autre réciproque :
Un cercle donné, trouver un triangle ABC tels que les 6 points soient sur ce cercle.
Ce cercle des 6 points a un nom : Cercle de Conway. Voir ![]()
Et pour une réciproque un peu plus compliquée : ![]() et
et ![]()

 Cliquez pour afficher
Cliquez pour afficher