Bonjour,
as-tu fait un dessin ?...
es-tu en 4ème en France ? je te pose cette question car ce sujet est passé plusieurs fois sur l' mais avec niveau 2nds

Non je n'ai pas fais de dessin et je vis sur l'île de la Réunion et c'est bien un livre de 4è (Transmath p.93). Il y a juste un petit schéma technique dans l livre symbolisant la zone de baignade uniquement.
Merci d'avance !

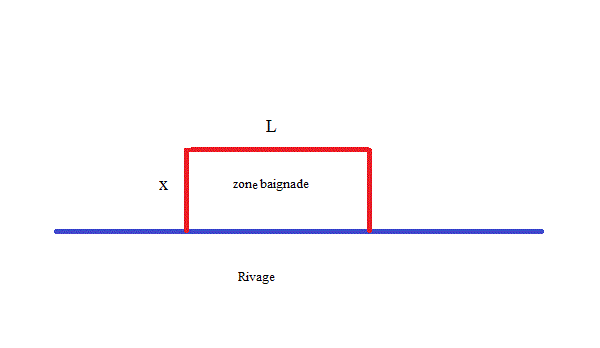
voici le schéma, je pense que ça correspond à celui que tu as...

x désignant la largeur de la zone de baignade :

calcule L en fonction de x
puis
exprime l'aire du rectangle en fonction de x

Sur mon schèma il n'y a aucune mesure , juste dans le texte il y'a écrit que la longueur de la ligne d'eau égale 150m :/

bonjour,
x=largeur
150=2x+ L
150-2x=L


A(piscine)=(150-2x)*x
=150x-2x²

Un moyen plus simple svp ? Je comprends pas vraiment.

J'ai compris Merci Beaucoup a vous !

Bonsoir Clems et Tilk.
Soit x le côté perpendiculaire au bord de mer. Le côté parallèle mesure 150-2x.
La zone mesure x(150-2x) = 150x-2x² m².
150x-2x² doit être le plus grand possible, donc 2x²-150x le plus petit possible, de même que x²-75x
n²-bn = [n² - 2(b/2)n + (b/2)²] - (b/2)² = (n - b/2)² -(b/2)²
en transposant à x²-75x
x²-75x = (x-37,5)²-37,5²
(x-37,5)² doit être le plus petit possible, donc être nul
solution x = 37,5
Le côté perpendiculaire au rivage mesure 37,5 m; le côté parallèle au rivage mesure 75 m; la zone de baignade mesure 2812,5 m².

Que représentent B et N ? O.o

Bonjour
Vous avez eu la correction du dm ?

Bonjour Clarisse16
je doute fort queClems te réponde....il ou elle n'est plus sur l'

Si tu veux de l'aide, crée ton propre message avec l'énoncé complet de ton exercice