Inscription / Connexion Nouveau Sujet
Somme dans une Suite Arithmétique
Bonjour,
J'ai cet exercice pour un DM en classe de Première Générale Spé Maths.
Voici l'énoncé :
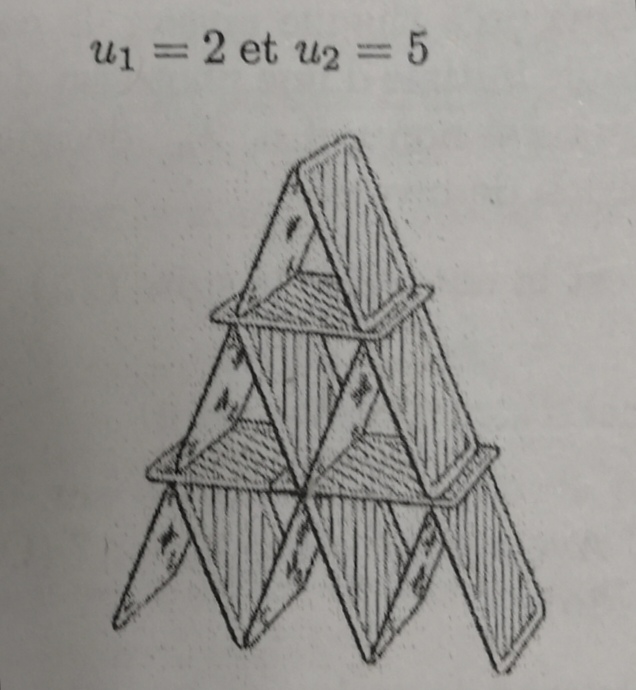
On construit un château de cartes sous le modèle ci-dessous et on note un le nombre de cartes nécessaires pour construire l'étage n ainsi que la base soutenant l'étage situé au dessus. On numérote Les étages de haut en bas. Avec cette notation : u1 = 2 et u2 = 5
(a) Calculez le nombre de cartes de l'étage 5. J'ai trouvé 14.
(b) Calculez le nombre total de cartes pour réaliser un château de 5 étages. J'ai trouvé 40.
(c) Exprimer un en fonction de n. J'ai trouvé : 2n+(n-1), soit 3n-1
(d) Montrer que pour un château de n étages on utilise au total : (3n²+n)/2 cartes. À l'aide de la formule de mon cours, [(uk+un)(n-k+1)]/2, j'ai trouvé [(u1+un)(n-1+1)]/2, soit au final (2n+un²)/2, ce qui ne correspond pas au résultat demandé. (je peux donner les étapes intermédiaires si besoin).
(e) Un château compte au total 1190 cartes. Combien a-t-il d'étages ? Je n'ai absolument aucune idée de comment faire.
Vous l'aurez deviné, j'aurais besoin d'aide pour la question (d) et (e), merci d'avance 😁

Le bouton "X2" permet de mettre en indice.
(Écrire l'indice entre les balises "sub" et "/sub" qui apparaissent, ou taper d'abord l'indice, puis le sélectionner avant d'utiliser le bouton)
Le bouton "X2" permet de mettre en indice.
Il est fortement conseillé de faire "Aperçu" avant "POSTER".
Merci Leile, je vais essayer !
Sylvieg, merci, mais je suis sur téléphone, c'est un peu dur.
Je vous tiens au courant de si j'y arrive !
Cependant, je n'ai toujours pas d'idée pour répondre à la question (e), je vous remercie d'avance si vous pouvez m'aider !
Pour e) :
pour un château de n étages on utilise au total : (3n²+n)/2 cartes
Un château compte au total 1190 cartes
Bonjour,
Après de multiples tentatives, je reste bloqué, pour le e), à :
(3n²+n)/2 = 1190
3n²+n = 1190/2 = 2380
et là, plus rien... je ne sais pas comment progresser à partir de cette étape...
Merci d'avance

D'accord.
Tu sais que n est un entier.
Deux méthodes :
n(3n+1) = 2380 implique que n divise 2380.
Et que le second facteur, 3n+1, est supérieur à n, et environ 3 fois n.
Chercher un diviseur de 2380 proche de ( 2380)/3.
2380)/3.
Avec ta calculatrice ou un tableur, entrer la fonction f définie par 3x2+x.
Afficher les valeurs de f(x) pour x = 1, 2, 3, ....
Jusqu'à ce que 2380 soit atteint.

 n / 2.
n / 2.


