Bonsoir Sylvieg.

 Cliquez pour afficher

En utilisant on voit que les quatre faces ont la même aire.
La suite en découle facilement :
le volume du tétraèdre ABCD est la somme des volumes des tétraèdres ABCM, BCDM, CDAM et ABDM.

C'est tout bon

 Cliquez pour afficher

En fait les faces sont des triangles isométriques

Je suis vraiment bête.

Là, tu as tout faux !

Belle généralisation de cet exercice : Distances dans un tétraèdre

Puisque la mèche est un peu vendue, je rajoute une autre question :
Un tétraèdre dont les quatre faces sont des triangles de même aire est un tétraèdre dont les quatre faces sont des triangles isométriques.
Qui donnera la démonstration la plus simple de cette propriété ?
Inutile de blanker.

Bonjour,

Je n'invente rien ...

Soit le milieu de l'arête .
Les points sont projetés orthogonalement sur l'arête en :



Avec Thalès, est milieu de .

et

  Donc puis avec Pythagore :



Le triangle est isocèle en et

On a montré que si les 4 faces d'un tétraèdre ont la même aire, la perpendiculaire commune à deux arêtes opposées passe par leurs milieux.
Par exemple avec une symétrie par rapport à la droite
Bref, les arêtes opposées d'un tel tétraèdre sont égales et leurs faces sont isométriques.

Un peu plus algébrique:

Le trétraèdre est défini par :



La somme des distances d'un point à l'intérieur du tétraèdre à ses faces est donnée par:



Elle est donc constante pour a, b, c donné.

Je reviens juste sur mon "Thalès de l'espace" un peu olé-olé.
Si on n'est pas convaincu, on peut imaginer 3 plans parallèles et équidistants. Toute droite sécante avec ces 3 plans détermine deux segments égaux en particulier toute droite perpendiculaire à ces plans.
Je pense qu'on peut dire aussi plus sèchement qu'une projection de l'espace sur une droite conserve les rapports de longueur

@LittleFox,
Plus algébrique, mais joli quand même

@lake,
Moi non plus, je n'ai rien inventé. Sauf cette question :
Quels sont les tétraèdres dont les faces ont la même aire ?
Ne trouvant rien seule, j'ai fait une recherche sur la toile.
La réponse est : Les tétraèdres dont les faces sont isométriques.

Pour la démonstration, je n'ai pas vu de démonstration plus simple que celle que tu proposes.
Thalès au départ ne me semble pas olé olé.
Mais invoquer des plans parallèles et équidistants peut plus facilement convaincre un lycéen.

Bonjour Syvieg,

Après avoir posté 12h48, j'ai fouiné et trouvé ceci : sur le site de Diophante où tu pourras trouver de nombreuses solutions dont une de Julia Paule qui me plait beaucoup

Oui, j'avais trouvé ce site avec la solution de Pierre Renfer.
Je n'y vois pas de Julia Paule.

Mince, j'ai confondu ; je voulais dire Catherine Nadault

J'avais vu cette solution aussi ; mais elle fait appel à des prérequis que je ne maitrise pas bien.
Je trouve cette affirmation un peu olé olé :
"Comme la perpendiculaire à ce plan menée par I est la perpendiculaire commune aux arêtes AB et DC"
La démonstration de 12h48 me semble plus simple, s'appuyant sur des notions élémentaires de géométrie dans l'espace.
Bien que toutes les deux fassent intervenir la notion de perpendiculaire commune à deux droites non parallèles

Bonsoir,
Je me suis inspirée de la figure de Catherine Nadault pour donner une démonstration un peu différente.
J'ai tenté de n'utiliser dans l'espace que des notions élémentaires.
Ce n'est pas vraiment satisfaisant

Donnée : Un tétraèdre ABCD qui vérifie aire(ABC) = aire(ABD).

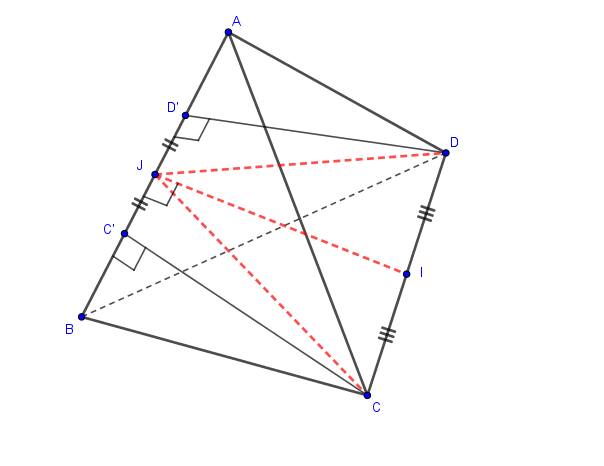
Dans la figure, les droites (C₁C₂) et (D₁D₂) sont les parallèles à (AB) issues des points C et D.
Les triangles dessinés sont tous dans des plans perpendiculaires à la droite (AB).
Deux plans parallèles coupent un troisième plan en deux droites parallèles.
D'où des rectangles en pagaille.
Les longueurs CC' et DD' sont égales car hauteurs issues de C et D dans les triangles ABC et ABD qui ont la même aire.
Tous les triangles représentés sur la figure sont donc isocèles.
Les points Q et R sont les milieux de [C₁D₁] et [C₂D₂]. La droite (QR) est parallèle (AB).
Dans le plan (C₁C₂D₂D₁), d'après Thalès la droite (QR) coupe [CD] et [C₃D₃] en leur milieu I.
Le triangle JC₃D₃ est dans un plan perpendiculaire à (AB).
La droite (IJ) est donc perpendiculaire à (AB).
Le triangle JC₃D₃ est isocèle ; sa médiane (IJ) est donc aussi hauteur.
La droite (IJ) est perpendiculaire aux droites (QR) et (C₃D₃) qui sont deux droites concourantes du plan (C₁C₂D₂D₁) ; la droite (IJ) est donc perpendiculaire à ce plan, donc à la droite (CD).
La perpendiculaire commune aux droites (AB) et (CD) passe donc par le milieu I de [CD].