Inscription / Connexion Nouveau Sujet
Sous-variété
Bonsoir,
J'ai besoin d'aide sur la deuxième question de cet exercice.
Soit a>0 réel. Notons U l'intervalle ]1,∞[ de R, et soit f de U dans R² définie par
1. Montrer que f est une immersion de classe C∞.
2. La partie f(U) est-elle une sous-variété de R²?
1) La dimension de l'espace de départ est inférieure à la dimension de l'espace l'arrivé , donc f peut-être une immersion ,mais pas une submersion.
De plus, ona :
Ce jacobien ne peut-être nul d'où f est une immersion.
2. Je n'arrive pas à montrer le 2) je ne sais pas comment montrer qu'une partie est une sv lorsqu'elle est définie par paramétrisation.
Merci de m'aider !
Bonjour,
J'ai essayer d'appliquer la définition par paramétrisation d'une sous-variété :
M est une sous-variété de R^n si:
Pour tout x de M, il existe un ouvert U de R^n contenant x, un ouvert V de R^m contenant 0 et une immersion en 0 g de V dans R^n telle que g(0)=x et g induit un homéomorphisme de V dans (U inter M).
J'ai essayer de considéré l'immersion f, mais je ne vois pas clairement les choses.
Bonjour
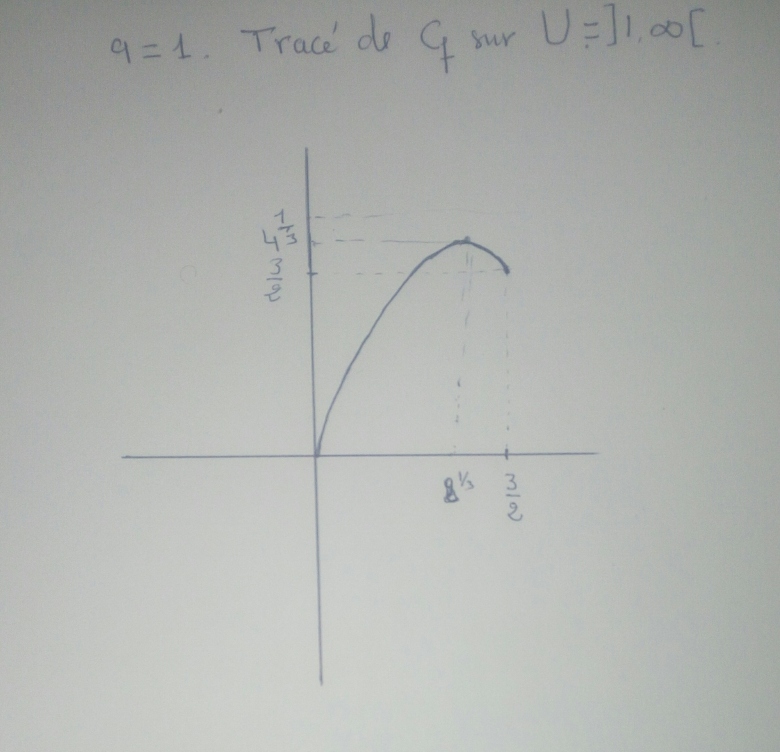
Commence par faire le dessin pour a=1. Tu obtiens une espèce de 8 en (0,0). Montre qu'aucun voisinage de (0,0) ne peut être homéomorphe à un segment. C'est un argument de connexité qui fonctionne.
Oui, cette partie est bien telle que tu la présentes et c'est bien une sous-variété. Tu eux simplement prouver que la projection sur l'axe Ox est un homéomorphisme.
Ma réponse (trop rapide) parlait de l'image complète , qui est l'exmple type d'image d'une immersion injective qui n'est pas une sous-variété.
Bonjour Camélia
Donc je dois juste montrer que g: U ---> f(U) définie par g(t)=f(t) est un homéomorphisme ?


 géométrie en post-bac
géométrie en post-bac